
【題目】圖是一個![]() 的方格(其中心的方格線已被劃去).一只青蛙停在
的方格(其中心的方格線已被劃去).一只青蛙停在![]() 格處,從某一時刻起,青蛙每隔一秒鐘就跳到與它所在方格有公共邊的另一方格內,直至跳到
格處,從某一時刻起,青蛙每隔一秒鐘就跳到與它所在方格有公共邊的另一方格內,直至跳到![]() 格才停下..若青蛙經過每一個方格不超過一次,則青蛙的跳法總數為________.
格才停下..若青蛙經過每一個方格不超過一次,則青蛙的跳法總數為________.

【答案】26
【解析】
如圖,分兩種情況討論.
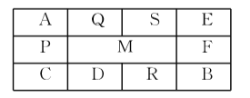
(1)如果青蛙不經過![]() 格,則有2條路徑:
格,則有2條路徑:![]() ,
,![]() .
.
(2)如果青蛙經過![]() 格,若某時刻青蛙跳到
格,若某時刻青蛙跳到![]() 格,則它下一秒內一定跳至
格,則它下一秒內一定跳至![]() 格;若某時刻青蛙跳到
格;若某時刻青蛙跳到![]() 格,則它下一秒內一定不會跳至
格,則它下一秒內一定不會跳至![]() 格.因此,可將
格.因此,可將![]() 、
、![]() 兩格合并為一個大方格(設之為
兩格合并為一個大方格(設之為![]() ).同樣地,可將
).同樣地,可將![]() 、
、![]() 兩格合并為大方格
兩格合并為大方格![]() .
.
如果兩個方格有公共邊,則在兩個方格間連上虛線,如圖9.
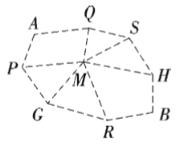
由圖可知,![]() 、
、![]() 、
、![]() 和
和![]() 、
、![]() 、
、![]() 對稱地分布在直線
對稱地分布在直線![]() 的兩側.
的兩側.
顯然,青蛙第一步必跳入![]() 、
、![]() 兩格中的某格,倒數第二步必跳入
兩格中的某格,倒數第二步必跳入![]() 、
、![]() 兩格中的某格.
兩格中的某格.
如果青蛙第一步跳至![]() 格,倒數第二步跳至
格,倒數第二步跳至![]() 格,那么,這樣的路徑有3條:
格,那么,這樣的路徑有3條:![]() ,
,![]() ,
,![]() .
.
如果青蛙第一步跳至![]() 格,倒數第二步跳至
格,倒數第二步跳至![]() 格,設青蛙第
格,設青蛙第![]() 秒鐘跳至
秒鐘跳至![]() 格,第
格,第![]() 秒跳至
秒跳至![]() 格,第
格,第![]() 秒跳至
秒跳至![]() 格.
格.
則![]() 格可以是
格可以是![]() 、
、![]() 、
、![]() 、
、![]() 格可以是
格可以是![]() 、
、![]() 、
、![]() .因此,這樣的路徑有
.因此,這樣的路徑有![]() 條.
條.
由對稱性知,如果青蛙第一步跳至![]() 格,倒數第二步跳至
格,倒數第二步跳至![]() 格,則這樣的路徑有3條;如果青蛙第一步跳
格,則這樣的路徑有3條;如果青蛙第一步跳![]() 格,倒數第二步跳至
格,倒數第二步跳至![]() 格,則這樣的路徑有9條.
格,則這樣的路徑有9條.
綜上,青蛙的跳法總數為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某單位從一所學校招收某類特殊人才.對![]() 位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
位已經選拔入圍的學生進行運動協調能力和邏輯思維能力的測試,其測試結果如下表:
| 一般 | 良好 | 優秀 |
一般 |
|
|
|
良好 |
|
|
|
優秀 |
|
|
|
例如表中運動協調能力良好且邏輯思維能力一般的學生是![]() 人.由于部分數據丟失,只知道從這
人.由于部分數據丟失,只知道從這![]() 位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為
位參加測試的學生中隨機抽取一位,抽到邏輯思維能力優秀的學生的概率為![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)從運動協調能力為優秀的學生中任意抽取![]() 位,求其中至少有一位邏輯思維能力優秀的學生的概率.
位,求其中至少有一位邏輯思維能力優秀的學生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某年數學競賽請自以為來自X星球的選手參加填空題比賽,共10道題目,這位選手做題有一個古怪的習慣:先從最后一題(第10題)開始往前看,凡是遇到會的題就作答,遇到不會的題目先跳過(允許跳過所有的題目),一直看到第1題;然后從第1題開始往后看,凡是遇到先前未答的題目就隨便寫個答案,遇到先前已答的題目則跳過(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答題),這樣所有的題目均有作答,設這位選手可能的答題次序有n種,則n的值為( )
A.512B.511C.1024D.1023
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設銳角![]() 的外接圓的半徑為
的外接圓的半徑為![]() ,在
,在![]() 內取外接圓的同心圓
內取外接圓的同心圓![]() ,其半徑為
,其半徑為![]()
![]() ,從圓
,從圓![]() 上任取一點
上任取一點![]() ,作
,作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .
.
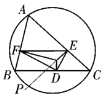
(1)求證:![]() 的面積為定值;
的面積為定值;
(2)猜想:當![]() 為任意三角形、同心圓
為任意三角形、同心圓![]() 為任意同心圓時,結論是否成立(不要求證明)?
為任意同心圓時,結論是否成立(不要求證明)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在測試中,客觀題難度的計算公式為![]() ,其中
,其中![]() 為第
為第![]() 題的難度,
題的難度, ![]() 為答對該題的人數,
為答對該題的人數, ![]() 為參加測試的總人數.現對某校高三年級240名學生進行一次測試,共5道客觀題,測試前根據對學生的了解,預估了每道題的難度,如表所示:
為參加測試的總人數.現對某校高三年級240名學生進行一次測試,共5道客觀題,測試前根據對學生的了解,預估了每道題的難度,如表所示:
題號 | 1 | 2 | 3 | 4 | 5 |
考前預估難度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
測試后,從中隨機抽取了20名學生的答題數據進行統計,結果如表:

(Ⅰ)根據題中數據,估計中240名學生中第5題的實測答對人數;
(Ⅱ)從抽樣的20名學生中隨機抽取2名學生,記這2名學生中第5題答對的人數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅲ)試題的預估難度和實測難度之間會有偏差.設![]() 為第
為第![]() 題的實測難度,請用
題的實測難度,請用![]() 和
和![]() 設計一個統計量,并制定一個標準來判斷本次測試對難度的預估是否合理.
設計一個統計量,并制定一個標準來判斷本次測試對難度的預估是否合理.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】田忌賽馬是![]() 史記
史記![]() 中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等
中記載的一個故事,說的是齊國將軍田忌經常與齊國眾公子賽馬,孫臏發也們的馬腳力都差不多,都分為上、中、下三等![]() 于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注
于是孫臏給田忌將軍制定了一個必勝策略:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得公子們許多賭注![]() 假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
假設田忌的各等級馬與某公子的各等級馬進行一場比賽獲勝的概率如表所示:
田忌的馬 | 上等馬 | 中等馬 | 下等馬 |
上等馬 |
|
| 1 |
中等馬 |
|
|
|
下等馬 | 0 |
|
|
比賽規則規定:一次比由三場賽馬組成,每場由公子和田忌各出一匹馬出騫,結果只有勝和負兩種,并且毎一方三場賽馬的馬的等級各不相同,三場比賽中至少獲勝兩場的一方為最終勝利者.
![]() 如果按孫臏的策略比賽一次,求田忌獲勝的概率;
如果按孫臏的策略比賽一次,求田忌獲勝的概率;
![]() 如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com