
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() 是自然對數的底數.
是自然對數的底數.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)若函數![]() 在區間
在區間![]() 上為單調函數,求
上為單調函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,試判斷方程
時,試判斷方程![]() 是否有實數解,并說明理由.
是否有實數解,并說明理由.
【答案】(1)極小值為![]() ,無極大值
,無極大值
(2)![]() 或
或![]()
(3)無實根,理由見解析
【解析】
(1)當![]() 時,求導數,確定函數的單調性,即可求函數
時,求導數,確定函數的單調性,即可求函數![]() 的極值;
的極值;
(2)函數![]() 在區間
在區間![]() 上為單調函數等價于
上為單調函數等價于![]() 或
或![]() 在區間
在區間![]() 上恒成立,再利用分離變量最值法即可得解;
上恒成立,再利用分離變量最值法即可得解;
(3)當![]() 時,
時,![]() 可變形為
可變形為![]() ,再左右分別構造函數求最值即可得解.
,再左右分別構造函數求最值即可得解.
解:(1)當![]() 時,
時,
![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
即函數![]() 的減區間為
的減區間為![]() ,增區間為
,增區間為![]() ,
,
即函數的極小值為![]() ,無極大值;
,無極大值;
(2)由函數![]() ,
,
則![]() ,
,
由函數![]() 在區間
在區間![]() 上為單調函數,
上為單調函數,
則![]() 或
或![]() 在區間
在區間![]() 上恒成立,
上恒成立,
即![]() 或
或![]() 在區間
在區間![]() 上恒成立,
上恒成立,
設![]() ,
,![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,
即函數![]() 在
在![]() 為減函數,
為減函數,
則![]() ,
,
即![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
故![]() 的取值范圍為
的取值范圍為![]() 或
或![]() ;
;
(3)當![]() 時,方程
時,方程![]() 沒有實數解
沒有實數解
理由如下:
當![]() 時,
時,![]() ,
,
則![]() 即為
即為![]() ,
,
令![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
即函數![]() 的增區間為
的增區間為![]() ,減區間為
,減區間為![]() ,
,
即![]() ,
,
即![]() ,
,
令![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
即函數![]() 的增區間為
的增區間為![]() ,減區間為
,減區間為![]() ,
,
即![]() ,
,
則![]() ,
,
即![]() 無實數解,
無實數解,
故當![]() 時,方程
時,方程![]() 沒有實數解.
沒有實數解.


科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且與直線l:
,且與直線l:![]() 相切.
相切.
(1)求動圓圓心的軌跡C的方程;
(2)過F作斜率為![]() 的直線m與C交于兩點A,B,過A,B分別作C的切線,兩切線交點為P,證明:點P始終在直線l上且
的直線m與C交于兩點A,B,過A,B分別作C的切線,兩切線交點為P,證明:點P始終在直線l上且![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 交于點
交于點![]() ,曲線
,曲線![]() 與
與![]() 軸交于點
軸交于點![]() ,求線段
,求線段![]() 的中點到點
的中點到點![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天干地支,簡稱為干支,源自中國遠古時代對天象的觀測.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”稱為十天干,“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”稱為十二地支.干支紀年法是天干和地支依次按固定的順序相互配合組成,以此往復,60年為一個輪回.現從農歷2000年至2019年共20個年份中任取2個年份,則這2個年份的天干或地支相同的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=3sin(﹣3x![]() )﹣2的圖象向右平移
)﹣2的圖象向右平移![]() 個單位長度得到函數g(x)的圖象,若g(x)在區間[
個單位長度得到函數g(x)的圖象,若g(x)在區間[![]() ,θ]上的最大值為1,則θ的最小值為( )
,θ]上的最大值為1,則θ的最小值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ax+b,g(x)=ex(cx+d),若曲線y=f(x)和曲線y=g(x)都過點P(0,2),且在點P處有相同的切線y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2時,恒有f(x)≤kg(x),求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() (
(![]() ),下列結論正確的是( )
),下列結論正確的是( )
①當![]() 時,
時,![]() 恒成立;②當
恒成立;②當![]() 時,
時,![]() 的零點為
的零點為![]() 且
且![]() ;③當
;③當![]() 時,
時,![]() 是
是![]() 的極值點;④若
的極值點;④若![]() 有三個零點,則實數k的取值范圍為
有三個零點,則實數k的取值范圍為![]() .
.
A.①②④B.①③C.②③④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古建筑中的窗飾是藝術和技術的統一體,給人于美的享受.如圖(1)為一花窗;圖(2)所示是一扇窗中的一格,呈長方形,長30 cm,寬26 cm,其內部窗芯(不含長方形邊框)用一種條形木料做成,由兩個菱形和六根支條構成,整個窗芯關于長方形邊框的兩條對稱軸成軸對稱.設菱形的兩條對角線長分別為x cm和y cm,窗芯所需條形木料的長度之和為L.
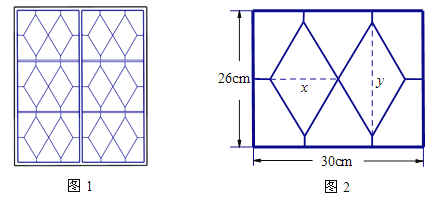
(1)試用x,y表示L;
(2)如果要求六根支條的長度均不小于2 cm,每個菱形的面積為130 cm2,那么做這樣一個窗芯至少需要多長的條形木料(不計榫卯及其它損耗)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com