【題目】設各項均為正數的數列
的前
項和為
，已知
，且
對一切
都成立.
(1)當
時.
①求數列的通項公式；
②若
，求數列
的前項的和
；
(2)是否存在實數
，使數列是等差數列.如果存在，求出的值；若不存在，說明理由.
科目：高中數學 來源： 題型：
【題目】某市2010年4月1日—4月30日對空氣污染指數的監測數據如（主要污染物為可吸入顆粒物）：61，76，70，56，81，91，92，91，75，81，88，67，101，103，95，91，77，86，83，82，82，64，79，86，85，75，71，49，45．
樣本頻率分布表：
分組 | 頻數 | 頻率 |
[41，51） | 2 | |
[51，61） | 1 | |
[61，71） | 4 | |
[71，81） | 6 | |
[81，91） | 10 | |
[91，101） | ||
[101，111） | 2 |
（1） 完成頻率分布表；
（2）作出頻率分布直方圖；
（3）根據國家標準，污染指數在0~50之間時，空氣質量為優：在51~100之間時，為良；在101~150之間時，為輕微污染；在151~200之間時，為輕度污染．請你依據所給數據和上述標準，對該市的空氣質量給出一個簡短評價.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線T的焦點為F，準線為l，過F的直線m與T交于A，B兩點，C，D分別為A，B在l上的射影，M為AB的中點，若m與l不平行，則△CMD是( )
A. 等腰三角形且為銳角三角形
B. 等腰三角形且為鈍角三角形
C. 等腰直角三角形
D. 非等腰的直角三角形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，函數
.
（1）求實數
的值，使得
為奇函數；
（2）若關于
的方程
有兩個不同實數解，求的取值范圍；
（3）若關于的不等式
對任意
恒成立，求的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
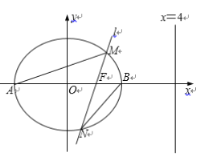
【題目】如圖，已知橢圓
的離心率為
，右準線方程為
，
、
分別是橢圓
的左、右頂點，過右焦點
且斜率為
的直線
與橢圓相交于
，
兩點.
（1）求橢圓的標準方程.
（2）記
、
的面積分別為
、
，若
，求
的值；
（3）設線段
的中點為
，直線
與右準線相交于點
，記直線
、
、
的斜率分別為
、
、
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對由
和
這兩個數字組成的字符串,作如下規定:按從左向右的順序,當第一個子串“
”的最后一個所在數位是第
(
,且
)位,則稱子串“”在第位出現;再繼續從第
位按從左往右的順序找子串“”,若第二個子串“”的最后一個所在數位是第
位(其中
且
),則稱子串“”在第位出現;……;如此不斷地重復下去.如:在字符串
中,子串“”在第
位和第
位出現,而不是在第
位和第
位出現.記在
位由
組成的所有字符串中,子串“”在第位出現的字符串的個數為
.
（1）求
的值;
（2）求證:對任意的正整數,
是
的倍數.
查看答案和解析>>
科目：高中數學 來源： 題型：
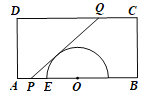
【題目】某生態農場有一矩形地塊，地塊內有一半圓形池塘（如圖所示），其中
百米，
百米，半圓形池塘的半徑為1百米，圓心
與線段
的中點重合，半圓與的左側交點為
.該農場計劃分別在
和
上各選一點
，修建道路
，要求
與半圓相切.
（1）若
，求該道路的總長；
（2）若
為觀光道路，修建費用是4萬元/百米，
為便道，修建費用是1萬元/百米，求修建觀光道路與便道的總費用的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（多選題）下列說法中，正確的命題是（ ）
A.已知隨機變量
服從正態分布
，
，則
．
B.以模型
去擬合一組數據時，為了求出回歸方程，設
，將其變換后得到線性方程
，則
，
的值分別是
和0.3．
C.已知兩個變量具有線性相關關系，其回歸直線方程為
，若
，
，
，則
．
D.若樣本數據
，
，…，
的方差為2，則數據
，
，…，
的方差為16．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
