
| A. | -$\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{1}{2}$ |
分析 由已知得:$\left\{\begin{array}{l}{f(x)+2f(\frac{1}{x})=2x+1}\\{f(\frac{1}{x})+2f(x)=\frac{2}{x}+1}\end{array}\right.$,解得f(x)=$\frac{4}{3x}-\frac{2x}{3}+\frac{1}{3}$,由此能求出f(2).
解答 解:∵函數f(x)滿足f(x)+2f($\frac{1}{x}$)=2x+1,①
∴f($\frac{1}{x}$)+2f(x)=$\frac{2}{x}+1$,②
聯立①②,得:$\left\{\begin{array}{l}{f(x)+2f(\frac{1}{x})=2x+1}\\{f(\frac{1}{x})+2f(x)=\frac{2}{x}+1}\end{array}\right.$,
解得f(x)=$\frac{4}{3x}-\frac{2x}{3}+\frac{1}{3}$,
∴f(2)=$\frac{4}{6}-\frac{4}{3}+\frac{1}{3}$=-$\frac{1}{3}$.
故選:A.
點評 本題考查函數值的求法,是基礎題,解題時要認真審題,注意函數性質的合理運用.


科目:高中數學 來源: 題型:填空題
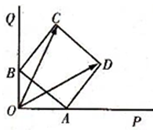 如圖,邊長為2的正方形ABCD的頂點A,B分別在兩條互相垂直的射線OP,OQ上滑動,則$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值為8.
如圖,邊長為2的正方形ABCD的頂點A,B分別在兩條互相垂直的射線OP,OQ上滑動,則$\overrightarrow{OC}$•$\overrightarrow{CD}$的最大值為8.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x∈N,使得$\frac{1}{{x}^{2}+x+1}$≤0 | B. | ?x0∈N,使得$\frac{1}{{{x}_{0}}^{2}+{x}_{0}+1}$≤0 | ||
| C. | ?x∈N,使得x2+x+1≤0 | D. | ?x0∈N,使得x02+x0+1≤0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com