
【題目】已知函數f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)試用含a的代數式表示b;
(2)求f(x)的單調區間;
(3)令a=﹣1,設函數f(x)在x1、x2(x1<x2)處取得極值,記點M(x1,f(x1)),N(x2,f(x2)).證明:線段MN與曲線f(x)存在異于M,N的公共點.
【答案】(1)b=2a﹣1.(2)見解析(3)見解析
【解析】
(1)求導得到f′(x)=x2+2ax+b,代入數據計算得到答案.
(2)討論a>1,a=1和a<1三種情況,分別計算得到答案.
(3)f′(x)=x2﹣2x﹣3=0,得x1=﹣1,x2=3,得到函數單調區間,得到MN的方程為y![]() x﹣1,計算F(0)=3>0,F(2)=﹣3<0,得到答案.
x﹣1,計算F(0)=3>0,F(2)=﹣3<0,得到答案.
(1)依題意,得f′(x)=x2+2ax+b.由f′(﹣1)=1﹣2a+b=0得b=2a﹣1.
(2)f(x)![]() x3+ax2+(2a﹣1)x,故f′(x)=x2+2ax+2a﹣1=(x+1)(x+2a﹣1).
x3+ax2+(2a﹣1)x,故f′(x)=x2+2ax+2a﹣1=(x+1)(x+2a﹣1).
令f′(x)=0,則x=﹣1或x=1﹣2a.
①當a>1時,1﹣2a<﹣1.
當x變化時,f′(x)與f(x)的變化情況如下表:
x | (﹣∞,1﹣2a) | (1﹣2a,﹣1) | (﹣1,+∞) |
f′(x) | + | ﹣ | + |
f(x) | 單調遞增 | 單調遞減 | 單調遞增 |
得,函數f(x)的單調增區間為(﹣∞,1﹣2a)和(﹣1,+∞),單調減區間為(1﹣2a,﹣1).
②當a=1時,1﹣2a=﹣1.此時,f′(x)≥0恒成立,且僅在x=﹣1處f′(x)=0,故函數f(x)的單調增區間為(﹣∞,+∞).
③當a<1時,1﹣2a>﹣1,同理可得函數f(x)的單調增區間為(﹣∞,﹣1)和(1﹣2a,+∞),單調減區間為(﹣1,1﹣2a).
綜上所述:當a>1時,函數f(x)的單調增區間為(﹣∞,1﹣2a)和(﹣1,+∞),單調減區間為(1﹣2a,﹣1);
當a=1時,函數f(x)的單調增區間為(﹣∞,+∞);
當a<1時,函數f(x)的單調增區間為(﹣∞,﹣1)和(1﹣2a,+∞),單調減區間為(﹣1,1﹣2a).
(3)當a=﹣1時,得f(x)![]() x3﹣x2﹣3x.
x3﹣x2﹣3x.
由f′(x)=x2﹣2x﹣3=0,得x1=﹣1,x2=3.
由(2)得f(x)的單調增區間為(﹣∞,﹣1)和(3,+∞),單調減區間為(﹣1,3),
所以函數f(x)在x1=﹣1,x2=3處取得極值.故M(﹣1,![]() ),N(3,﹣9).
),N(3,﹣9).
所以直線MN的方程為y![]() x﹣1.
x﹣1.
由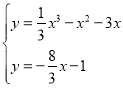 得x3﹣3x2﹣x+3=0.
得x3﹣3x2﹣x+3=0.
令F(x)=x3﹣3x2﹣x+3.
易得F(0)=3>0,F(2)=﹣3<0,而F(x)的圖象在(0,2)內是一條連續不斷的曲線,
故F(x)在(0,2)內存在零點x0,這表明線段MN與曲線f(x)有異于M,N的公共點.


科目:高中數學 來源: 題型:
【題目】(2017高考新課標Ⅲ,理19)如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
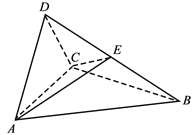
(1)證明:平面ACD⊥平面ABC;
(2)過AC的平面交BD于點E,若平面AEC把四面體ABCD分成體積相等的兩部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在衡陽市“創全國文明城市”(簡稱“創文”)活動中,市教育局對本市A,B,C,D四所高中學校按各校人數分層抽樣,隨機抽查了200人,將調查情況進行整理后制成下表:
學校 | A | B | C | D |
抽查人數 | 10 | 15 | 100 | 75 |
“創文”活動中參與的人數 | 9 | 10 | 80 | 49 |
假設每名高中學生是否參與“創文”活動是相互獨立的
(1)若本市共8000名高中學生,估計C學校參與“創文”活動的人數;
(2)在上表中從A,B兩校沒有參與“創文”活動的同學中隨機抽取2人,求恰好A,B兩校各有1人沒有參與“創文”活動的概率;
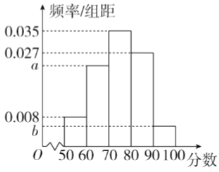
(3)在隨機抽查的200名高中學生中,進行文明素養綜合素質測評(滿分為100分),得到如上的頻率分布直方圖,其中![]() .求a,b的值,并估計參與測評的學生得分的中位數.(計算結果保留兩位小數).
.求a,b的值,并估計參與測評的學生得分的中位數.(計算結果保留兩位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解高二年級中華傳統文化經典閱讀的整體情況,從高二年級隨機抽取10名學生進行了兩輪測試,并把兩輪測試成績的平均分作為該名學生的考核成績.記錄的數據如下:
1號 | 2號 | 3號 | 4號 | 5號 | 6號 | 7號 | 8號 | 9號 | 10號 | |
第一輪測試成績 | 96 | 89 | 88 | 88 | 92 | 90 | 87 | 90 | 92 | 90 |
第二輪測試成績 | 90 | 90 | 90 | 88 | 88 | 87 | 96 | 92 | 89 | 92 |
(Ⅰ)從該校高二年級隨機選取一名學生,試估計這名學生考核成績大于90 分的概率;
(Ⅱ)從考核成績大于90分的學生中再隨機抽取兩名同學,求這兩名同學兩輪測試成績均大于等于90分的概率;
(Ⅲ)記抽取的10名學生第一輪測試的平均數和方差分別為![]() ,
,![]() ,考核成績的平均數和方差分別為
,考核成績的平均數和方差分別為![]() ,
,![]() ,試比較
,試比較![]() 與
與![]() ,
, ![]() 與
與![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 是定義為R的偶函數,且
是定義為R的偶函數,且![]() 對任意的
對任意的![]() ,都有
,都有![]() 且當
且當![]() 時,
時, ![]() ,若在區間
,若在區間![]() 內關于
內關于![]() 的方程
的方程![]() 恰好有3個不同的實數根,則
恰好有3個不同的實數根,則![]() 的取值范圍是 ( )
的取值范圍是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓柱體木材的橫截面半徑為![]() ,從該木材中截取一段圓柱體,再加工制作成直四棱柱
,從該木材中截取一段圓柱體,再加工制作成直四棱柱![]() ,該四棱柱的上、下底面均為等腰梯形,分別內接于圓柱的上、下底面,下底面圓的圓心
,該四棱柱的上、下底面均為等腰梯形,分別內接于圓柱的上、下底面,下底面圓的圓心![]() 在梯形
在梯形![]() 內部,
內部,![]() ,
,![]() ,
,![]() ,設
,設![]() .
.
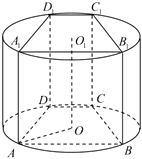
(1)求梯形![]() 的面積;
的面積;
(2)當![]() 取何值時,直四棱柱
取何值時,直四棱柱![]() 的體積最大?并求出最大值(注:木材的長度足夠長)
的體積最大?并求出最大值(注:木材的長度足夠長)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為![]() (φ為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
(φ為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() .
.
(1)直線l與曲線C是否有公共點?并說明理由;
(2)若直線l與兩坐標軸的交點為A,B,點P是曲線C上的一點,求△PAB的面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com