
【題目】已知曲線C的參數方程為![]() (φ為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
(φ為參數),以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() .
.
(1)直線l與曲線C是否有公共點?并說明理由;
(2)若直線l與兩坐標軸的交點為A,B,點P是曲線C上的一點,求△PAB的面積的最大值.
【答案】(1)沒有交點,理由見詳解;(2)3![]() .
.
【解析】
(1)將曲線![]() 的參數方程化為普通方程,將直線
的參數方程化為普通方程,將直線![]() 的極坐標方程化為直角方程,聯立方程組,根據
的極坐標方程化為直角方程,聯立方程組,根據![]() 的情況,求得兩曲線的相交情況;
的情況,求得兩曲線的相交情況;
(2)由(1)中所求,容易得點![]() 的坐標,設點
的坐標,設點![]() 坐標為(3cosθ,sinθ),再將問題轉化為三角函數值域的問題即可求得.
坐標為(3cosθ,sinθ),再將問題轉化為三角函數值域的問題即可求得.
(1)曲線C的參數方程為![]() (φ為參數),
(φ為參數),
轉換為直角坐標方程為![]() .
.
直線l的極坐標方程為![]() ,
,
整理得![]() ,
,
轉換為直角坐標方程為x﹣y﹣6=0,
聯立方程組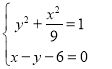
消去![]() ,可得10y2+12y+27=0,
,可得10y2+12y+27=0,
由于△=122﹣4×10×27<0,所以直線與橢圓沒有交點.
(2)直線的直角坐標方程為x﹣y﹣6=0,
與x軸的交點A(6,0)與y軸的交點坐標為B(0,6),
所以|AB|![]() ,
,
設橢圓上點P的坐標為(3cosθ,sinθ),
所以點P到直線l的距離d
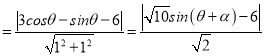 ,
,
當![]() 時,
時,![]() ,
,
則![]() 3
3![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】“搜索指數”是網民通過搜索引擎,以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大,表示網民對該關鍵詞的搜索次數越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數變化的走勢圖.

根據該走勢圖,下列結論正確的是( )
A. 這半年中,網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看,去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() x3+ax2+bx,且f′(﹣1)=0.
x3+ax2+bx,且f′(﹣1)=0.
(1)試用含a的代數式表示b;
(2)求f(x)的單調區間;
(3)令a=﹣1,設函數f(x)在x1、x2(x1<x2)處取得極值,記點M(x1,f(x1)),N(x2,f(x2)).證明:線段MN與曲線f(x)存在異于M,N的公共點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() 和
和![]() 是函數
是函數![]() 的圖象與
的圖象與![]() 軸的2個相鄰交點的橫坐標,且當
軸的2個相鄰交點的橫坐標,且當![]() 時,
時,![]() 取得最大值2.
取得最大值2.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)將函數![]() 的圖象上的每一點的橫坐標變為原來的
的圖象上的每一點的橫坐標變為原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象,再將函數
的圖象,再將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以平面直角坐標系
為參數),以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,橢圓
軸的正半軸為極軸建立極坐標系,橢圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程(寫成一般式)和橢圓
的普通方程(寫成一般式)和橢圓![]() 的直角坐標方程(寫成標準方程);
的直角坐標方程(寫成標準方程);
(2)若直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,且與
兩點,且與![]() 軸相交于點
軸相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本小題滿分13分)
工作人員需進入核電站完成某項具有高輻射危險的任務,每次只派一個人進去,且每個人只派一次,工作時間不超過10分鐘,如果有一個人10分鐘內不能完成任務則撤出,再派下一個人.現在一共只有甲、乙、丙三個人可派,他們各自能完成任務的概率分別![]()
![]() ,假設
,假設![]() 互不相等,且假定各人能否完成任務的事件相互獨立.
互不相等,且假定各人能否完成任務的事件相互獨立.
(1)如果按甲在先,乙次之,丙最后的順序派人,求任務能被完成的概率.若改變三個人被派出的先后順序,任務能被完成的概率是否發生變化?
(2)若按某指定順序派人,這三個人各自能完成任務的概率依次為![]() ,其中
,其中![]() 是
是![]() 的一個排列,求所需派出人員數目
的一個排列,求所需派出人員數目![]() 的分布列和均值(數字期望)
的分布列和均值(數字期望)![]() ;
;
(3)假定![]() ,試分析以怎樣的先后順序派出人員,可使所需派出的人員數目的均值(數字期望)達到最小.
,試分析以怎樣的先后順序派出人員,可使所需派出的人員數目的均值(數字期望)達到最小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com