
| A. | (-∞,1] | B. | [1,+∞) | C. | (-∞,0] | D. | [0,+∞) |
分析 由?x1∈[$\frac{1}{2}$,3],都?x2∈[2,3],使得f(x1)≥g(x2),可得f(x)在x1∈[$\frac{1}{2}$,3]的最小值不小于g(x)在x2∈[2,3]的最小值,構造關于a的不等式,可得結論.
解答 解:當x1∈[$\frac{1}{2}$,3]時,由f(x)=x+$\frac{4}{x}$得,f′(x)=$\frac{{x}^{2}-4}{{x}^{2}}$,
令f′(x)>0,解得:x>2,令f′(x)<0,解得:x<2,
∴f(x)在[$\frac{1}{2}$,2]單調遞減,在(2,3]遞增,
∴f(2)=4是函數的最小值,
當x2∈[2,3]時,g(x)=2x+a為增函數,
∴g(2)=a+4是函數的最小值,
又∵?x1∈[$\frac{1}{2}$,3],都?x2∈[2,3],使得f(x1)≥g(x2),
可得f(x)在x1∈[$\frac{1}{2}$,3]的最小值不小于g(x)在x2∈[2,3]的最小值,
即4≥a+4,解得:a≤0,
故選:C
點評 本題以命題的真假判斷與應用為載體,考查的知識是指數函數以及對勾函數函數的圖象和性質,考察導數的應用,函數的單調性問題,本題是一道中檔題.


科目:高中數學 來源: 題型:選擇題
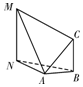 如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從M點測得A點的俯角∠NMA=30°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°;已知山高BC=200m,則山高MN=( )
如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從M點測得A點的俯角∠NMA=30°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°;已知山高BC=200m,則山高MN=( )| A. | 300m | B. | 200$\sqrt{2}$m | C. | 200$\sqrt{3}$m | D. | 300$\sqrt{2}$m |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[{\frac{1}{13},2}]$ | B. | [$\frac{2}{13}$,1] | C. | $[{\frac{1}{6},6}]$ | D. | $[{\frac{1}{3},3}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
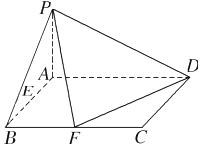 已知在四棱錐P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分別是線段AB、BC的中點.
已知在四棱錐P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分別是線段AB、BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| T(分鐘) | 25 | 30 | 35 | 40 |
| 頻數(次) | 100 | 150 | 200 | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com