
| A. | y=|x| | B. | $y=-\frac{1}{x}$ | C. | y=2-x | D. | y=x3 |
分析 逐一分析給定四個函數在定義域上的單調性,可得答案.
解答 解:函數y=|x|=$\left\{\begin{array}{l}-x,x<0\\ x,x≥0\end{array}\right.$,在(-∞,0)上是減函數,故A不滿足條件;
函數$y=-\frac{1}{x}$的圖象不連續,在(-∞,0)上和在(0,+∞)上均為增函數,但在定義域內不是單調遞增函數,故B不滿足條件;
函數y=2-x在定義域內是單調遞減函數,故C不滿足條件;
函數y=x3滿足y′=3x2≥0恒成立,故在定義域內是單調遞減函數,故D滿足條件;
故選:D
點評 本題考查的知識點是利用導數研究函數的單調性,熟練掌握各種基本初等函數的單調性,是解答的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=($\frac{1}{3}$)|x| | C. | f(x)=sinx-x | D. | f(x)=$\frac{lnx}{x}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
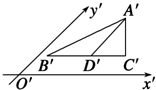 如圖所示的是水平放置的三角形直觀圖,D′是△A′B′C′中B′C′邊上的一點,且D′離C′比D′離B′近,又A′D′∥y′軸,那么原△ABC的AB、AD、AC三條線段中 ( )
如圖所示的是水平放置的三角形直觀圖,D′是△A′B′C′中B′C′邊上的一點,且D′離C′比D′離B′近,又A′D′∥y′軸,那么原△ABC的AB、AD、AC三條線段中 ( )| A. | 最長的是AB,最短的是AC | B. | 最長的是AC,最短的是AB | ||
| C. | 最長的是AB,最短的是AD | D. | 最長的是AD,最短的是AC |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com