
【題目】 由an與Sn的關系求通項公式
(1)已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]()
![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)已知正項數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() (
(![]() ).求數列
).求數列![]() 的通項公式;
的通項公式;
(3)已知數列{an}的前n項和為Sn,a1=1,Sn=2an+1,求Sn
(4)已知正項數列![]() 中,
中,![]() ,
,![]() ,前n項和為
,前n項和為![]() ,且滿足
,且滿足![]() (
(![]() ).求數列
).求數列![]() 的通項公式;
的通項公式;
(5)設數列{an}的前n項積為Tn,且Tn+2an=2(n∈N*).數列![]() 是等差數列;求數列
是等差數列;求數列![]() 的通項公式;
的通項公式;
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) 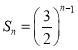 ; (4)
; (4) ![]() (5)
(5) ![]()
【解析】
(1)利用通項與前![]() 項和的關系分
項和的關系分![]() 與
與![]() 時分析求解即可.
時分析求解即可.
(2)利用通項與前![]() 項和的關系分
項和的關系分![]() 與
與![]() 時分析求解即可
時分析求解即可
(3)根據![]() 得出關于
得出關于![]() 的遞推公式判斷出
的遞推公式判斷出![]() 為等比數列再求解即可.
為等比數列再求解即可.
(4)兩邊同乘以![]() 再化簡證明當
再化簡證明當![]() 時
時![]() 即可.
即可.
(5)分別取![]() ,利用
,利用![]() 是等差數列求解即可.
是等差數列求解即可.
(1)當![]() 時,
時, ![]() ,即
,即![]() .
.
當![]() 時,
時, ![]() …①
…①
![]() …②
…②
①-②得![]()
![]() .
.
當![]() 時也滿足上式.
時也滿足上式.
故![]() ,
,![]()
(2)由題,![]()
當![]() 時,
時, ![]() ,解得
,解得![]() .
.
當![]() 時,
時, ![]() …①
…①
![]() …②
…②
①-②可得![]() ,化簡得
,化簡得![]() ,
,
因為正項數列![]() ,故
,故![]() ,
,
故![]() 是以
是以![]() 為首項,2為公差的等差數列.
為首項,2為公差的等差數列.
故![]()
(3)由題,![]() ,即
,即![]() ,故
,故![]() 是以
是以![]() 為首項,
為首項,![]() 為公比的等比數列.故
為公比的等比數列.故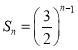
(4)因為![]() ,即
,即![]() ,故
,故![]() ,
,
又正項數列![]() ,故
,故![]() ,即
,即![]() ,
,![]() .
.
故![]() .
.
(5)因為![]() ,且
,且![]() 是等差數列.
是等差數列.
令![]() 時有
時有![]() .
.
令![]() 時有
時有![]() ,
,
故![]() ,
,![]() ,故
,故![]() ,
,![]() .
.
又![]() 是等差數列,故
是等差數列,故![]() 是以
是以![]() ,公差
,公差![]() 的等差數列.
的等差數列.
故![]() ,故
,故![]() .
.
又![]() 的前
的前![]() 項積為
項積為![]() ,故當
,故當![]() 時
時![]() .
.
故![]() .
.![]()
當![]() 時
時![]() 也滿足.
也滿足.
故![]() ,
,![]()


科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 所在平面與等邊
所在平面與等邊![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
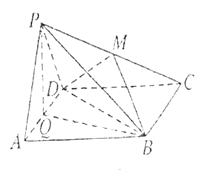
(1)求證:![]() 平面
平面![]() .
.
(2)試問:在線段![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,試指出點
?若存在,試指出點![]() 的位置,并證明你的結論:若不存在,請說明理由.
的位置,并證明你的結論:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《九章算術商功》中闡述:“斜解立方,得兩塹堵.斜解塹堵,其一為陽馬,一為鱉臑.陽馬居二,鱉臑居一,不易之率也.合兩鱉臑三而一,驗之以棊,其形露矣.”若稱為“陽馬”的某幾何體的三視圖如圖所示,圖中網格紙上小正方形的邊長為1,對該幾何體有如下描述:
①四個側面都是直角三角形;
②最長的側棱長為![]() ;
;
③四個側面中有三個側面是全等的直角三角形;
④外接球的表面積為24π.
其中正確的描述為____.
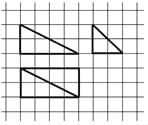
查看答案和解析>>
科目:高中數學 來源: 題型:
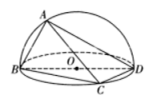
【題目】如圖,已知![]() 是圓
是圓![]() 的直徑,
的直徑,![]() ,
,![]() 在圓上且分別在
在圓上且分別在![]() 的兩側,其中
的兩側,其中![]() ,
,![]() .現將其沿
.現將其沿![]() 折起使得二面角
折起使得二面角![]() 為直二面角,則下列說法不正確的是( )
為直二面角,則下列說法不正確的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一個球面上
在同一個球面上
B.當![]() 時,三棱錐
時,三棱錐![]() 的體積為
的體積為![]()
C.![]() 與
與![]() 是異面直線且不垂直
是異面直線且不垂直
D.存在一個位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com