Question

3．已知橢圓M：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），短軸的一個頂點與一個焦點的距離為2，離心率為$\frac{\sqrt{3}}{2}$．
（1）求橢圓M的方程；
（2）過橢圓M的中心作直線l與橢圓交于P、Q兩點，且∠PF₂Q=$\frac{2π}{3}$，設橢圓的左、右焦點分別為F₁、F₂
①判斷四邊形F₁PF₂Q的形狀；
②求△PF₂Q的面積．

Answer 1

分析 （1）由題意求得a，再由離心率得到c，結合隱含條件求得b，則橢圓方程可求；
（2）①由橢圓的對稱性可得，四邊形F₁PF₂Q是平行四邊形；
②先求出|PF₁|、|PF₂|的距離，根據對稱性可知|PF₁|=|QF₂|，再由三角形面積公式可得到答案．

解答 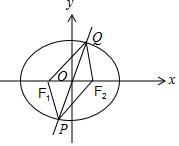解：（1）由題意可得a=2，再由e=$\frac{c}{a}=\frac{\sqrt{3}}{2}$，得c=$\sqrt{3}$，
∴b²=a²-c²=1，則橢圓方程為$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（2）如圖，
①由橢圓的對稱性可得，四邊形F₁PF₂Q是平行四邊形；
②由①得，四邊形PF₁QF₂是平行四邊形．
∴△PF₂Q的面積等于△PF₁F₂的面積．
∵∠PF₂Q=$\frac{2π}{3}$，∴∠PF₁Q=$\frac{π}{3}$，
設|PF₁|=r₁，|PF₂|=r₂，
則$\left\{\begin{array}{l}{{r}_{1}+{r}_{2}=4}\\{{{r}_{1}}^{2}+{{r}_{2}}^{2}-{r}_{1}{r}_{2}=12}\end{array}\right.$，∴${r}_{1}{r}_{2}=\frac{4}{3}$．
∴${S}_{△P{F}_{2}Q}={S}_{△{F}_{2}P{F}_{1}}$=$\frac{1}{2}{r}_{1}{r}_{2}$•sin$\frac{π}{3}$=$\frac{\sqrt{3}}{3}$．

點評 本題考查橢圓的簡單性質，直線與橢圓的綜合應用，直線與圓的位置關系，考查分析問題解決問題的能力，是中檔題．