解(Ⅰ)函數(shù)f(x)=

•

=(2cosωx,

sinωx)•(cosωx,2cosωx)
=2cos
2ωx+2

sinωxcosωx
=2sin(2ωx+

)+1.
∴T=
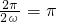
,ω=1,
∴f(x)=2sin(2x+

)+1,…(3分)
∵2kπ
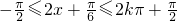
?
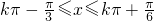
k∈Z
f(x)的單調(diào)增區(qū)間[
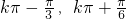
]k∈Z….(6分)
(Ⅱ)∵在△ABC中,a、b、c分別是角A、B、C的對(duì)邊,f(A)=2,
∴2sin(2A+

)+1=2,
∴sin(2A+

)=

,
2A+

=

,
∴A=

,
∴S
△ABC=
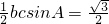
,∵b=1
∴c=2.
由余弦定理a
2=b
2+c
2-2bccosA?a=

,
由正弦定理

?
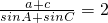
…..(12分)
分析:(Ⅰ) 利用斜率的數(shù)量積已經(jīng)二倍角公式兩角和的正弦函數(shù)化簡(jiǎn)函數(shù)的表達(dá)式,利用函數(shù)的周期求出ω,通過(guò)正弦函數(shù)的單調(diào)增區(qū)間求解f(x)的單調(diào)增區(qū)間.
(Ⅱ) 在△ABC中,a、b、c分別是角A、B、C的對(duì)邊,利用f(A)=2結(jié)合(Ⅰ)求出A,通過(guò)b=1,△ABC的面積為

,求出c,利用余弦定理求出a,通過(guò)正弦定理求
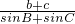
的值.
點(diǎn)評(píng):本題是中檔題,考查三角函數(shù)的化簡(jiǎn)求值,斜率的數(shù)量積的應(yīng)用,正弦定理與余弦定理的應(yīng)用,考查計(jì)算能力.

 =(2cosωx,
=(2cosωx, sinωx),
sinωx), =(cosωx,2cosωx)(w>0),函數(shù)f(x)=
=(cosωx,2cosωx)(w>0),函數(shù)f(x)= •
• 的最小正周期為π:
的最小正周期為π: ,求
,求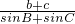 的值.
的值. •
• =(2cosωx,
=(2cosωx, sinωx)•(cosωx,2cosωx)
sinωx)•(cosωx,2cosωx) sinωxcosωx
sinωxcosωx )+1.
)+1.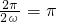 ,ω=1,
,ω=1, )+1,…(3分)
)+1,…(3分)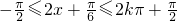 ?
?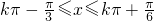 k∈Z
k∈Z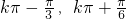 ]k∈Z….(6分)
]k∈Z….(6分) )+1=2,
)+1=2, )=
)= ,
, =
= ,
, ,
,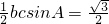 ,∵b=1
,∵b=1 ,
, ?
?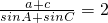 …..(12分)
…..(12分) ,求出c,利用余弦定理求出a,通過(guò)正弦定理求
,求出c,利用余弦定理求出a,通過(guò)正弦定理求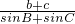 的值.
的值.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案