
如圖,在三棱柱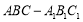 中,側面
中,側面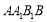 為菱形, 且
為菱形, 且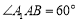 ,
,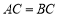 ,
,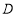 是
是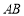 的中點.
的中點.
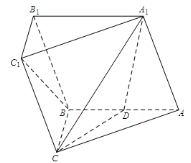
(1)求證:平面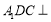 平面
平面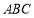 ;
;
(2)求證: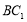 ∥平面
∥平面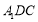 .
.
(1)詳見解析,(2)詳見解析.
【解析】
試題分析:(1)證明面面垂直,關鍵找出線面垂直.因為側面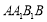 為菱形, 且
為菱形, 且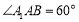 ,所以△
,所以△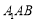 為正三角形,因而有
為正三角形,因而有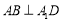 .又
.又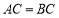 ,
,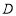 是
是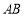 的中點,所以有
的中點,所以有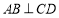 ,這樣就可得到
,這樣就可得到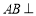 平面
平面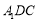 ,進而可證平面
,進而可證平面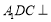 平面
平面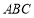 .(2)證明線面平行,關鍵找出線線平行. 條件“
.(2)證明線面平行,關鍵找出線線平行. 條件“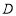 是
是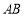 的中點”,提示找中位線.取
的中點”,提示找中位線.取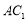 中點
中點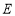 ,就可得
,就可得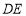 ∥
∥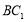 ,利用線面平行判斷定理即可.解決此類問題,需注意寫全定理成立的所有條件,不可省略.
,利用線面平行判斷定理即可.解決此類問題,需注意寫全定理成立的所有條件,不可省略.
試題解析:(1)證明:∵  為菱形,且
為菱形,且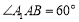 ,
,
∴△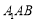 為正三角形. 2分
為正三角形. 2分

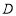 是
是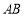 的中點,∴
的中點,∴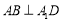 .
.
∵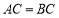 ,
,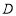 是
是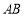 的中點,∴
的中點,∴ 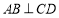 . 4分
. 4分

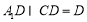 ,∴
,∴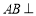 平面
平面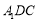 . 6分
. 6分
∵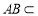 平面
平面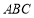 ,∴平面
,∴平面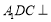 平面
平面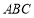 . 8分
. 8分
(2)證明:連結 ,設
,設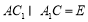 ,連結
,連結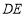 .
.
∵三棱柱的側面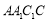 是平行四邊形,∴
是平行四邊形,∴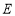 為
為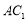 中點. 10分
中點. 10分
在△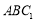 中,又∵
中,又∵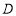 是
是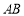 的中點,∴
的中點,∴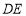 ∥
∥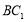 . 12分
. 12分
∵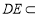 平面
平面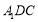 ,
,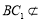 平面
平面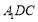 ,∴
,∴ 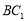 ∥平面
∥平面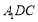 . 14分
. 14分
考點:面面垂直判定定理,線面平行判定定理


科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)理科數學試卷(解析版) 題型:解答題
甲乙兩個同學進行定點投籃游戲,已知他們每一次投籃投中的概率均為 ,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
,且各次投籃的結果互不影響.甲同學決定投5次,乙同學決定投中1次就停止,否則就繼續投下去,但投籃次數不超過5次.
(1)求甲同學至少有4次投中的概率;
(2)求乙同學投籃次數 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)理科數學試卷(解析版) 題型:填空題
從甲,乙,丙,丁4個人中隨機選取兩人,則甲乙兩人中有且只有一個被選取的概率為 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省蘇、錫、常、鎮四市高三教學情況調查(一)文科數學試卷(解析版) 題型:填空題
一個容量為20的樣本數據分組后,分組與頻數分別如下: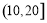 ,2;
,2;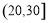 ,3;
,3;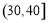 ,4;
,4;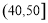 ,5;
,5; ,4;
,4;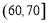 ,2.則樣本在
,2.則樣本在 上的頻率是 .
上的頻率是 .
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江蘇省淮安市高三5月信息卷文科數學試卷(解析版) 題型:解答題
在平面直角坐標系 中,已知橢圓的焦點在
中,已知橢圓的焦點在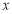 軸上,離心率為
軸上,離心率為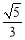 ,且經過點
,且經過點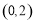 .
.
(1)求橢圓的標準方程;
(2) 以橢圓的長軸為直徑作圓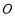 ,設
,設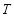 為圓
為圓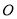 上不在坐標軸上的任意一點,
上不在坐標軸上的任意一點,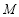 為
為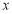 軸上一點,過圓心
軸上一點,過圓心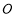 作直線
作直線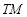 的垂線交橢圓右準線于點
的垂線交橢圓右準線于點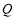 .問:直線
.問:直線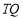 能否與圓
能否與圓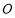 總相切,如果能,求出點
總相切,如果能,求出點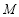 的坐標;如果不能,說明理由.
的坐標;如果不能,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com