試題分析:該幾何體是一正三棱柱,底面邊長為2,高為4,所以,底面三角形的高為

,其側(cè)視圖面積為4×

=

,故選B。
點評:基礎(chǔ)題,三視圖是高考必考題目,因此,要明確三視圖視圖規(guī)則,準(zhǔn)確地還原幾何體,明確幾何體的特征,以便進(jìn)一步解題。三視圖視圖過程中,要注意虛線的出現(xiàn),意味著有被遮掩的棱。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
一個幾何體的三視圖如右圖所示(單位長度:cm),則此幾何體的表面積是( )
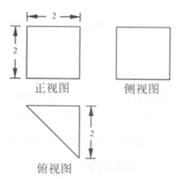
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知四棱錐
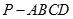
的底面是菱形.

,

為

的中點.

(1)求證:

∥平面

;
(2)求證:平面

平面

.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
四面體ABCD中,
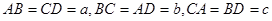
,則四面體ABCD外接球的半徑為
。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
如圖是一個幾何體的三視圖,則該幾何體為

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖(1),在等腰直角三角形

中,

,點

分別為線段

的中點,將

和

分別沿

折起,使二面角

和二面角

都成直二面角,如圖(2)所示。


(1)求證:

面

;
(2)求平面

與平面

所成的銳二面角的余弦值;
(3)求點

到平面

的距離。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
平行四邊形ABCD中,

·

=0,沿BD折成直二面角A一BD-C,且4AB
2 +2BD
2 =1,則三棱錐A-BCD的外接球的表面積為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
一個幾何體的三視圖如圖所示,則該幾何體的體積為
.

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,已知三棱柱ABC-A
1B
1C
1的側(cè)棱與底面垂直,AA
1=AB=AC=1,且AB⊥AC,M是CC
1的中點,N是BC的中點,點P在直線A
1B
1上,且滿足


(1)證明:PN⊥AM
(2)若
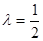
,求直線AA
1與平面PMN所成角的正弦值.
查看答案和解析>>




 中,
中, ,點
,點 分別為線段
分別為線段 的中點,將
的中點,將 和
和 分別沿
分別沿 折起,使二面角
折起,使二面角 和二面角
和二面角 都成直二面角,如圖(2)所示。
都成直二面角,如圖(2)所示。

 面
面 ;
; 與平面
與平面 所成的銳二面角的余弦值;
所成的銳二面角的余弦值; 到平面
到平面 的距離。
的距離。 ·
· =0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,則三棱錐A-BCD的外接球的表面積為( )
=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,則三棱錐A-BCD的外接球的表面積為( )





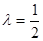 ,求直線AA1與平面PMN所成角的正弦值.
,求直線AA1與平面PMN所成角的正弦值.