
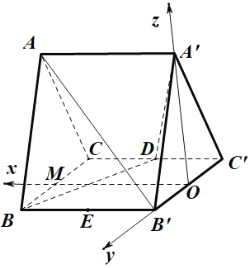
【題目】如圖,直三棱柱![]() 的所有棱長相等,
的所有棱長相等,![]() 為
為![]() 的中點.
的中點.
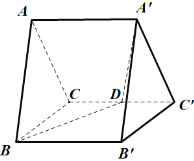
(1)求證:![]() 平面
平面![]() ;
;
(2)當![]() 是
是![]() 的中點時,求二面角
的中點時,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)設三棱柱的棱長為2,![]() 為
為![]() 的中點,連結
的中點,連結![]() ,易證
,易證![]() 平面
平面![]() ,取
,取![]() 的中點
的中點![]() ,連結
,連結![]() ,易知直線
,易知直線![]() 兩兩垂直,故以
兩兩垂直,故以![]() 為坐標原點,分別以射線
為坐標原點,分別以射線![]() 的方向為
的方向為![]() 軸的正方向,建立如圖所示的空間直角坐標系,從而可證明
軸的正方向,建立如圖所示的空間直角坐標系,從而可證明![]() ,
,![]() ,進而可證明
,進而可證明![]() 平面
平面![]() ;
;
(2)結合(1),分別求出平面![]() 、平面
、平面![]() 的法向量,然后利用空間向量法求出二面角
的法向量,然后利用空間向量法求出二面角![]() 的余弦值,進而可求出答案.
的余弦值,進而可求出答案.
(1)設三棱柱的棱長為2,![]() 為
為![]() 的中點,連結
的中點,連結![]() ,易知
,易知![]() ,又平面
,又平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,取
,取![]() 的中點
的中點![]() ,連結
,連結![]() ,易知直線
,易知直線![]() 兩兩垂直,故以
兩兩垂直,故以![]() 為坐標原點,分別以射線
為坐標原點,分別以射線![]() 的方向為
的方向為![]() 軸的正方向,建立如圖所示的空間直角坐標系,
軸的正方向,建立如圖所示的空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)知,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,![]() ,設平面
,設平面![]() 的法向量為
的法向量為![]() ,
,
則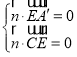 ,即
,即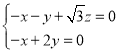 ,令
,令![]() ,可得
,可得![]() ,
,![]() ,可得平面
,可得平面![]() 的一個法向量
的一個法向量![]() ,
,
平面![]() 的一個法向量為
的一個法向量為![]() ,
,
設二面角![]() 的大小為
的大小為![]() ,則
,則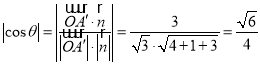 ,
,
則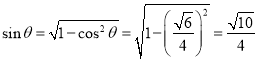 .
.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 為等邊三角形,邊長為2,
為等邊三角形,邊長為2,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面ABCD.
平面ABCD.
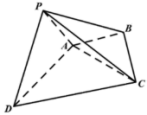
(1)證明:![]() 平面PAD;
平面PAD;
(2)求平面PAD與平面PBC所成銳二面角的余弦值;
(3)棱PD上是否存在一點E,使得![]() 平面PBC?若存在,求出
平面PBC?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心為原點O,焦點在x軸上的橢圓C的離心率為![]() ,且橢圓C的長軸是圓
,且橢圓C的長軸是圓![]() 的一條直徑.
的一條直徑.
(1)求橢圓C的方程;
(2)若不過原點的直線l與橢圓C交于A,B兩點,與圓M交于P、Q兩點,且直線OA,AB,OB的斜率成等比數列,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (
(![]() 為自然對數的底)。
為自然對數的底)。
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若存在均屬于區間![]() 的
的![]() ,
,![]() ,且
,且![]() ,使
,使![]() ,證明:
,證明:![]() ;
;
(Ⅲ)對于函數![]() 與
與![]() 定義域內的任意實數
定義域內的任意實數![]() ,若存在常數
,若存在常數![]() ,
,![]() ,使得
,使得![]() 和
和![]() 都成立,則稱直線
都成立,則稱直線![]() 為函數
為函數![]() 與
與![]() 的分界線。試探究當
的分界線。試探究當![]() 時,函數
時,函數![]() 與
與![]() 是否存在“分界線”?若存在,請給予證明,并求出
是否存在“分界線”?若存在,請給予證明,并求出![]() ,
,![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】西湖小學為了豐富學生的課余生活開設課后少年宮活動,其中面向二年級的學生共開設了三門課外活動課:七巧板、健美操、剪紙.203班有包括奔奔、果果在內的5位同學報名參加了少年宮活動,每位同學只能挑選一門課外活動課,已知每門課都有人選,則奔奔和果果選擇了同一個課外活動課的選課方法種數為( )
A.18B.36C.72D.144
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三角形![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 與半圓弧
與半圓弧![]() 所在的平面垂直,點
所在的平面垂直,點![]() 為半圓弧上異于
為半圓弧上異于![]() 的動點,
的動點,![]() 為
為![]() 的中點.
的中點.
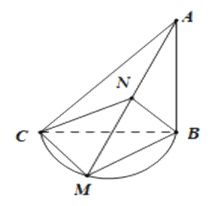
(1)求證:![]() ;
;
(2)當三棱錐![]() 體積最大時,求銳二面角
體積最大時,求銳二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com