
【題目】判斷下列函數的奇偶性.
(1)f(x)=x2-|x|+1,x∈[-1,4]; (2)f(x)= ;
;
(3)f(x)=![]() ; (4)f(x)=
; (4)f(x)=
【答案】見解析
【解析】(1)雖然f(-x)=f(x),但定義域不關于原點對稱,
故f(x)=x2-|x|+1,x∈[-1,4]是非奇非偶函數.
(2)由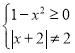 得-1≤x<0,或0<x≤1.
得-1≤x<0,或0<x≤1.
故函數f(x)的定義域為[-1,0)∪(0,1],關于原點對稱,
且有x+2>0.從而有f(x)=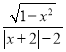 =
=![]() =
=![]() ,
,
于是f(-x)=-![]() =-f(x).故函數f(x)為奇函數.
=-f(x).故函數f(x)為奇函數.
(3)∵![]() ≥0,∴-1≤x<1.
≥0,∴-1≤x<1.
∴定義域不關于原點對稱.∴f(x)為非奇非偶函數.
(4)當x>0時,x<0 ,f(-x)=(-x)2+(-x)=x2-x;
當x<0時,x>0,f(-x)=-(-x)2+(-x)=-x2-x.
∴f(-x)=-f(x),∴f(x)是奇函數.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某制藥廠生產某種顆粒狀粉劑,由醫藥代表負責推銷,若每包藥品的生產成本為![]() 元,推銷費用為
元,推銷費用為![]() 元,預計當每包藥品銷售價為
元,預計當每包藥品銷售價為![]() 元時,一年的市場銷售量為
元時,一年的市場銷售量為![]() 萬包,若從民生考慮,每包藥品的售價不得高于生產成本的
萬包,若從民生考慮,每包藥品的售價不得高于生產成本的![]() ,但為了鼓勵藥品研發,每包藥品的售價又不得低于生產成本的
,但為了鼓勵藥品研發,每包藥品的售價又不得低于生產成本的![]()
(1) 寫出該藥品一年的利潤![]() (萬元)與每包售價
(萬元)與每包售價![]() 的函數關系式,并指出其定義域;
的函數關系式,并指出其定義域;
(2) 當每包藥品售價![]() 為多少元時,年利潤
為多少元時,年利潤![]() 最大,最大值為多少?
最大,最大值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每逢節假日,在微信好友群中發紅包逐漸成為一種時尚,還能增進彼此的感情,2016年春節期間,小魯在自己的微信好友群中,向在線的甲、乙、丙、丁四位好友隨機發放紅包,發放的規則為:每次發放一個,小魯自己不搶,每個人搶到的概率相同.
(1)若小魯隨機發放了3個紅包,求甲至少搶到一個紅包的概率;
(2)若丁因有事暫時離線一段時間,而小魯在這段時間內共發了3個紅包,其中2個紅包中各有10元,一個紅包中有5元.設這段時間內乙所得紅包的總錢數為![]() 元,求隨機變量
元,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓中心在坐標原點,A(2,0),B(0,1)是它的兩個頂點,直線y=kx(k>0)與AB相交于點D,與橢圓相交于E、F兩點.
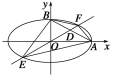
(1)若![]() =6
=6![]() ,求k的值;
,求k的值;
(2)求四邊形AEBF面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x-1|+|x-2a|.
(1)當a=1時,求f(x)≤3的解集;
(2)當x∈[1,2]時,f(x)≤3恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現從某班的一次期末考試中,隨機的抽取了七位同學的數學(滿分150分)、物理(滿分110分)成績如下表所示,數學、物理成績分別用特征量![]() 表示,
表示,
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求![]() 關于t的回歸方程;
關于t的回歸方程;
(2)利用(1)中的回歸方程,分析數學成績的變化對物理成績的影響,并估計該班某學生數學成績130分時,他的物理成績(精確到個位).
附:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:

![]() .
. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數![]() (m∈Z)為偶函數,且在區間(0,+∞)上是單調增函數.
(m∈Z)為偶函數,且在區間(0,+∞)上是單調增函數.
(1)求函數f(x)的解析式;
(2)設函數![]() ,若g(x)>2對任意的x∈R恒成立,求實數c的取值范圍.
,若g(x)>2對任意的x∈R恒成立,求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本著健康、低碳的生活理念,租用公共自行車的人越來越多.租用公共自行車的收費標準是每車每次不超過兩小時免費,超過兩小時的部分每小時2元(不足1小時的部分按1小時計算).甲乙兩人相互獨立租車(各租一車一次).設甲、乙不超過兩小時還車的概率分別為![]() ,
, ![]() ;兩小時以上且不超過三小時還車的概率分別為
;兩小時以上且不超過三小時還車的概率分別為![]() ,
, ![]() ;兩人租車時間都不會超過四小時.
;兩人租車時間都不會超過四小時.
(1)求出甲、乙所付租車費用相同的概率;
(2)設甲、乙兩人所付的租車費用之和為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的概率分布和期望.
的概率分布和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
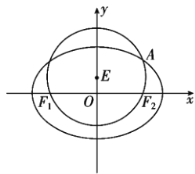
【題目】如圖,已知圓![]() :
: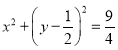 經過橢圓
經過橢圓![]() :
:![]() (
(![]() )的左右焦點
)的左右焦點![]() ,
,![]() ,與橢圓
,與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() ,
,![]() ,
,![]() 三點共線.
三點共線.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設與直線![]() (
(![]() 為原點)平行的直線
為原點)平行的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點.當
兩點.當![]() 的面積取到最大值時,求直線
的面積取到最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com