
【題目】定義在(﹣1,1)上的奇函數f(x)是減函數滿足f(1﹣a)+f(1﹣2a)<0,則a的取值范圍是 .
【答案】(0, ![]() )
)
【解析】解:由于定義在(﹣1,1)上的奇函數f(x)是減函數,滿足f(1﹣a)+f(1﹣2a)<0,
故有 f(1﹣a)<﹣f(1﹣2a)=f(2a﹣1),
∴ 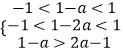 ,
,
解得 0<a< ![]() ,故a的取值范圍是(0,
,故a的取值范圍是(0, ![]() ).
).
所以答案是:(0, ![]() ).
).
【考點精析】掌握函數單調性的性質和函數奇偶性的性質是解答本題的根本,需要知道函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集;在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇.


科目:高中數學 來源: 題型:
【題目】為考察高中生的性別與喜歡數學課程之間的關系,在某學校高中生中隨機抽取了250名學生,得到如圖的二維條形圖.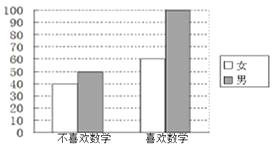
(1)根據二維條形圖,完成下表:
男 | 女 | 合計 | |
喜歡數學課程 | |||
不喜歡數學課程 | |||
合計 |
(2)對照如表,利用列聯表的獨立性檢驗估計,請問有多大把握認為“性別與喜歡數學有關系”?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x﹣1|+|x+1|,g(x)=|x﹣a|+|x+a|.
(Ⅰ)解不等式f(x)>9;
(Ⅱ)x1∈R,x2∈R,使得f(x1)=g(x2),求實數a的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+a(x﹣1)2,其中a>0.
(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;(2)討論函數f(x)的單調性;
(3)若函數f(x)有兩個極值點x1,x2,且x1<x2,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC內接于☉O,AB=AC,直線MN切☉O于點C,弦BD∥MN,AC與BD相交于點E. 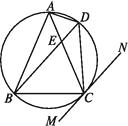
(1)求證:△ABE≌△ACD;
(2)求證:BE=BC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,圓錐SO的軸截面△SAB是邊長為4的正三角形,M為母線SB的中點,過直線AM作平面β⊥面SAB,設β與圓錐側面的交線為橢圓C,則橢圓C的短半軸長為( ) 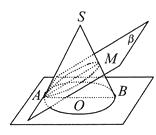
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是網絡工作者經常用來解釋網絡運作的蛇形模型:數字1出現在第1行;數字2,3出現在第2行;數字6,5,4(從左至右)出現在第3行;數字7,8,9,10出現在第4行,依此類推,則第20行從左至右的第4個數字應是 . 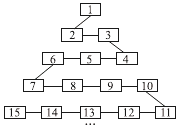
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com