
【題目】已知函數![]() .
.
(1)若![]() ,試判斷函數
,試判斷函數![]() 的零點個數;
的零點個數;
(2)若函數![]() 在
在![]() 上為增函數,求整數
上為增函數,求整數![]() 的最大值,(可能要用的數據:
的最大值,(可能要用的數據: ![]() ;
; ![]() ).
).
【答案】(1)1個;(2)6
【解析】試題分析:(Ⅰ)根據導數求解函數![]() 的單調性,利用零點的存在定理,即可判定函數
的單調性,利用零點的存在定理,即可判定函數![]() 在
在![]() 上的零點的個數.
上的零點的個數.
(Ⅱ)由題意,把![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上恒成立,進而轉化為
上恒成立,進而轉化為
![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,即
,即![]() ,利用導數求解函數
,利用導數求解函數![]() 的單調性和最小值,即可求解實數
的單調性和最小值,即可求解實數![]() 的取值范圍.
的取值范圍.
試題解析:
(1)因為![]() ,易知
,易知![]() 在
在![]() 上為增函數,則
上為增函數,則![]() ,
,
故![]() 在
在![]() 上為增函數,又
上為增函數,又![]() ,
, ![]() ,
,
所以函數![]() 在
在![]() 上的零點有且只有1個.
上的零點有且只有1個.
(2)因為![]() ,由題意
,由題意![]() 在
在![]() 上恒成立,
上恒成立,
因為![]() 顯然成立,故只需
顯然成立,故只需![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,則
,則![]()
因為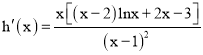
由(1)可知: ![]() 在
在![]() 上為增函數,故
上為增函數,故![]() 在
在![]() 上有唯一零點記為
上有唯一零點記為![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
則![]() ,
, ![]()
![]() ,
,
則![]() 在
在![]() 為減函數,
為減函數,
![]() 在
在![]() 為增函數,
為增函數,
故![]() 時,
時, ![]() 有最小值
有最小值![]() .
.
令![]() ,則
,則![]() 最小值有
最小值有![]()
![]() ,
,
因![]() ,則
,則![]() 的最小值大約在
的最小值大約在![]() 之間,故整數
之間,故整數![]() 的最大值為6.
的最大值為6.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
【題目】已知方程C:x2+y2﹣2x﹣4y+m=0,
(1)若方程C表示圓,求實數m的范圍;
(2)在方程表示圓時,該圓與直線l:x+2y﹣4=0相交于M、N兩點, ![]() ,求m的值;
,求m的值;
(3)在(2)的條件下,定點A(1,0),P在線段MN上運動,求直線AP的斜率取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】供電部門對某社區![]() 位居民2016年11月份人均用電情況進行統計后,按人均用電量分為
位居民2016年11月份人均用電情況進行統計后,按人均用電量分為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五組,整理得到如下的頻率分布直方圖,則下列說法錯誤的是( )
五組,整理得到如下的頻率分布直方圖,則下列說法錯誤的是( )
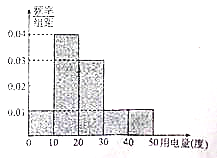
A. 11月份人均用電量人數最多的一組有![]() 人
人
B. 11月份人均用電量不低于![]() 度的有
度的有![]() 人
人
C. 11月份人均用電量為![]() 度
度
D. 在這![]() 位居民中任選
位居民中任選![]() 位協助收費,選到的居民用電量在
位協助收費,選到的居民用電量在![]() 一組的概率為
一組的概率為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據下列條件,求直線的方程:
(Ⅰ)過直線l1:2x﹣3y﹣1=0和l2:x+y+2=0的交點,且垂直于直線2x﹣y+7=0;
(Ⅱ)過點(﹣3,1),且在兩坐標軸上的截距之和為﹣4.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產甲、乙兩種產品,已知生產每噸甲、乙兩種產品所需煤、電力、勞動力、獲得利潤及每天資源限額(量大供應量)如下表所示:
資源\消耗量\產品 | 甲產品(每噸) | 乙產品(每噸) | 資源限額(每天) |
煤(t) | 9 | 4 | 360 |
電力(kwh) | 4 | 5 | 200 |
勞動力(個) | 3 | 10 | 300 |
利潤(萬元) | 6 | 12 |
問:每天生產甲、乙兩種產品各多少噸,獲得利潤總額最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程x2+y2﹣2(m+3)x+2(1﹣4m2)y+16m4+9=0表示一個圓.
(1)求實數m的取值范圍;
(2)求該圓半徑r的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AA1=4,AB=5,點D是AB的中點. 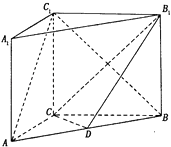
(1)求證:AC⊥BC1;
(2)求證:AC1∥平面CDB1 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com