【題目】已知向量 
與向量 
=（2，﹣1，2）共線，且滿足 =18，（k + ）⊥（k ﹣ ），求向量 及k的值．
【答案】解：∵ 
， 
共線，∴存在實數λ，使 =λ ，
∴ =λ 2=λ| |2 ， 解得λ=2．
∴ =2 =（4，﹣2，4）．
∵（k + ）⊥（k ﹣ ），
∴（k + ）（k ﹣ ）=（k +2 ）（k ﹣2 ）=0，
即（k2﹣4）| |2=0，
解得k=±2
【解析】由已知得存在實數λ，使 
=λ 
，由此能求出 =2 =（4，﹣2，4）．由（k + ）⊥（k ﹣ ），得（k2﹣4）| |2=0，由此能求出k=±2．
【考點精析】關于本題考查的數量積判斷兩個平面向量的垂直關系，需要了解若平面
的法向量為
，平面
的法向量為
，要證
，只需證
，即證
;即：兩平面垂直
兩平面的法向量垂直才能得出正確答案．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知數列
是公差為正數的等差數列，其前
項和為
，且
， 
．
（1）求數列
的通項公式；
（2）數列
滿足
， 
.①求數列
的通項公式；②是否存在正整數
， 
（
），使得
， 
， 
成等差數列？若存在，求出
， 
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
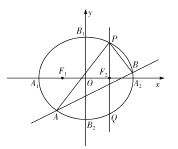
【題目】如圖，已知橢圓
的左、右頂點分別為
，上、下頂點分別為
，兩個焦點分別為
， 
，四邊形
的面積是四邊形
的面積的2倍.
（1）求橢圓
的方程；
（2）過橢圓
的右焦點且垂直于
軸的直線交橢圓
于
兩點， 
是橢圓
上位于直線
兩側的兩點.若直線
過點
，且
，求直線
的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學生在一門功課的22次考試中，所得分數莖葉圖如圖所示，則此學生該門功課考試分數的極差與中位數之和為（ ） 
A.117
B.118
C.118.5
D.119.5
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，梯形ABCD中，AD∥BC，AD⊥AB，AD=1，BC=2，AB=3，P是AB上的一個動點，∠CPB=α，∠DPA=β． （Ⅰ）當 
最小時，求tan∠DPC的值；
（Ⅱ）當∠DPC=β時，求 的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
