
【題目】已知函數 ![]() .
.
(1)求函數f(x)的單調增區間;
(2)若直線y=a與函數f(x)的圖象無公共點,求實數a的取值范圍.
【答案】
(1)解:函數 ![]() =cosx(
=cosx( ![]() cosx+
cosx+ ![]() sinx)
sinx)
= ![]() +
+ ![]() sin2x=
sin2x= ![]() cos(2x﹣
cos(2x﹣ ![]() )+
)+ ![]() ,
,
由2kπ﹣π≤2x﹣ ![]() ≤2kπ,k∈Z,
≤2kπ,k∈Z,
解得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
即f(x)的增區間為[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z;
],k∈Z;
(2)解:由(1)可得當2x﹣ ![]() =2kπ,即x=kπ+
=2kπ,即x=kπ+ ![]() ,k∈Z時,f(x)取得最大值
,k∈Z時,f(x)取得最大值 ![]() ;
;
當2x﹣ ![]() =2kπ+π,即x=kπ+
=2kπ+π,即x=kπ+ ![]() ,k∈Z時,f(x)取得最小值﹣
,k∈Z時,f(x)取得最小值﹣ ![]() .
.
由直線y=a與函數f(x)的圖象無公共點,
可得a的范圍是a> ![]() 或a<﹣
或a<﹣ ![]() .
.
【解析】(1)運用兩角差的余弦公式和二倍角公式,化簡可得f(x),再由余弦函數的單調區間,解不等式可得所求增區間;(2)求得f(x)的最值,即可得到a的取值范圍.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)=xex﹣ax2﹣x,a∈R.
(1)當a= ![]() 時,求函數f(x)的單調區間;
時,求函數f(x)的單調區間;
(2)若對x≥1時,恒有f(x)≥xex+ax2成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=alnx+x2(a為實常數).
(1)當a=﹣4時,求函數f(x)在[1,e]上的最大值及相應的x值;
(2)當x∈[1,e]時,討論方程f(x)=0根的個數.
(3)若a>0,且對任意的x1 , x2∈[1,e],都有 ![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點O,焦點在x軸上,離心率為 ![]() 的橢圓過點(
的橢圓過點( ![]() ,
, ![]() ).
). 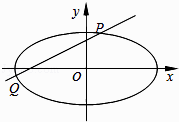
(1)求橢圓的方程;
(2)設不過原點O的直線l與該橢圓交于P,Q兩點,滿足直線OP,PQ,OQ的斜率依次成等比數列,求△OPQ面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD所在平面與三角形CDE所在的平面相交于CD,AE⊥平面CDE,且AE=1. 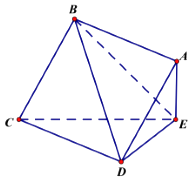
(1)求證:AB∥平面CDE;
(2)求證:DE⊥平面ABE;
(3)求點A到平面BDE的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差為2,前n項和為Sn , 且S1、S2、S4成等比數列.
(1)求數列{an}的通項公式;
(2)令bn=(﹣1)n﹣1 ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正四棱錐V﹣ABCD中,底面ABCD是邊長2為的正方形,其他四個側面都是側棱長為 ![]() 的等腰三角形.
的等腰三角形. 
(1)求正四棱錐V﹣ABCD的體積.
(2)求二面角V﹣BC﹣A的平面角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com