
【題目】已知函數f(x)=alnx+x2(a為實常數).
(1)當a=﹣4時,求函數f(x)在[1,e]上的最大值及相應的x值;
(2)當x∈[1,e]時,討論方程f(x)=0根的個數.
(3)若a>0,且對任意的x1 , x2∈[1,e],都有 ![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
【答案】
(1)解:當a=﹣4時,f(x)=﹣4lnx+x2,函數的定義域為(0,+∞).
![]() .
.
當x∈ ![]() 時,f′(x)0,
時,f′(x)0,
所以函數f(x)在 ![]() 上為減函數,在
上為減函數,在 ![]() 上為增函數,
上為增函數,
由f(1)=﹣4ln1+12=1,f(e)=﹣4lne+e2=e2﹣4,
所以函數f(x)在[1,e]上的最大值為e2﹣4,相應的x值為e
(2)解:由f(x)=alnx+x2,得 ![]() .
.
若a≥0,則在[1,e]上f′(x)>0,函數f(x)=alnx+x2在[1,e]上為增函數,
由f(1)=1>0知,方程f(x)=0的根的個數是0;
若a<0,由f′(x)=0,得x= ![]() (舍),或x=
(舍),或x= ![]() .
.
若 ![]() ,即﹣2≤a<0,f(x)=alnx+x2在[1,e]上為增函數,
,即﹣2≤a<0,f(x)=alnx+x2在[1,e]上為增函數,
由f(1)=1>0知,方程f(x)=0的根的個數是0;
若 ![]() ,即a≤﹣2e2,f(x)=alnx+x2在[1,e]上為減函數,
,即a≤﹣2e2,f(x)=alnx+x2在[1,e]上為減函數,
由f(1)=1,f(e)=alne+e2=e2+a≤﹣e2<0,
所以方程f(x)=0在[1,e]上有1個實數根;
若 ![]() ,即﹣2e2<a<﹣2,
,即﹣2e2<a<﹣2,
f(x)在 ![]() 上為減函數,在
上為減函數,在 ![]() 上為增函數,
上為增函數,
由f(1)=1>0,f(e)=e2+a.
![]() =
= ![]() .
.
當 ![]() ,即﹣2e<a<﹣2時,
,即﹣2e<a<﹣2時, ![]() ,方程f(x)=0在[1,e]上的根的個數是0.
,方程f(x)=0在[1,e]上的根的個數是0.
當a=﹣2e時,方程f(x)=0在[1,e]上的根的個數是1.
當﹣e2≤a<﹣2e時, ![]() ,f(e)=a+e2≥0,方程f(x)=0在[1,e]上的根的個數是2.
,f(e)=a+e2≥0,方程f(x)=0在[1,e]上的根的個數是2.
當﹣2e2<a<﹣e2時, ![]() ,f(e)=a+e2<0,方程f(x)=0在[1,e]上的根的個數是1
,f(e)=a+e2<0,方程f(x)=0在[1,e]上的根的個數是1
(3)解:若a>0,由(2)知函數f(x)=alnx+x2在[1,e]上為增函數,
不妨設x1<x2,則 ![]() 變為f(x2)+
變為f(x2)+ ![]() <f(x1)+
<f(x1)+ ![]() ,由此說明函數G(x)=f(x)+
,由此說明函數G(x)=f(x)+ ![]() 在[1,e]單調遞減,所以G′(x)=
在[1,e]單調遞減,所以G′(x)= ![]() ≤0對x∈[1,e]恒成立,即a
≤0對x∈[1,e]恒成立,即a ![]() 對x∈[1,e]恒成立,
對x∈[1,e]恒成立,
而 ![]() 在[1,e]單調遞減,所以a
在[1,e]單調遞減,所以a ![]() .
.
所以,滿足a>0,且對任意的x1,x2∈[1,e],都有 ![]() 成立的實數a的取值范圍不存在
成立的實數a的取值范圍不存在
【解析】(1)把a=﹣4代入函數解析式,求出函數的導函數,由導函數的零點把給出的定義[1,e]分段,判出在各段內的單調性,從而求出函數在[1,e]上的最大值及相應的x值;(2)把原函數f(x)=alnx+x2求導,分a≥0和a<0討論函數的單調性,特別是當a<0時,求出函數f(x)在[1,e]上的最小值及端點處的函數值,然后根據最小值和F(e)的值的符號討論在x∈[1,e]時,方程f(x)=0根的個數;(3)a>0判出函數f(x)=alnx+x2在[1,e]上為增函數,在規定x1<x2后把 ![]() 轉化為f(x2)+
轉化為f(x2)+ ![]() <f(x1)+
<f(x1)+ ![]() ,構造輔助函數G(x)=f(x)+
,構造輔助函數G(x)=f(x)+ ![]() ,由該輔助函數是減函數得其導函數小于等于0恒成立,分離a后利用函數單調性求a的范圍.
,由該輔助函數是減函數得其導函數小于等于0恒成立,分離a后利用函數單調性求a的范圍.
【考點精析】解答此題的關鍵在于理解函數的最大(小)值與導數的相關知識,掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值,以及對不等式的證明的理解,了解不等式證明的幾種常用方法:常用方法有:比較法(作差,作商法)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構造法,函數單調性法,數學歸納法等.
比較,其中最大的是一個最大值,最小的是最小值,以及對不等式的證明的理解,了解不等式證明的幾種常用方法:常用方法有:比較法(作差,作商法)、綜合法、分析法;其它方法有:換元法、反證法、放縮法、構造法,函數單調性法,數學歸納法等.


科目:高中數學 來源: 題型:
【題目】如圖,已知圓E:(x+ ![]() )2+y2=16,點F(
)2+y2=16,點F( ![]() ,0),P是圓E上任意一點.線段PF的垂直平分線和半徑PE相交于Q.
,0),P是圓E上任意一點.線段PF的垂直平分線和半徑PE相交于Q. 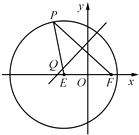
(1)求動點Q的軌跡Γ的方程;
(2)設直線l與(1)中軌跡Γ相交于A,B兩點,直線AO,l,OB的斜率分別為k1 , k,k2(其中k>0),若k1 , k,k2恰好構成公比不為1的等比數列,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解小學生的體能情況,抽取了某校一個年級的部分學生進行一分鐘跳繩次數測試,將所得的數據整理后,畫頻率分布直方圖.已知圖中橫軸從左向右的分組為[50,75)、[75,100)、[100,125)、[125,150],縱軸前3個對應值分別為0.004、0.01、0.02,因失誤第4個對應值丟失. 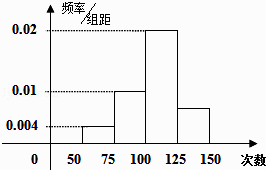
(Ⅰ) 已知第1小組頻數為10,求參加這次測試的人數?
(Ⅱ) 求第4小組在y軸上的對應值;
(Ⅲ) 若次數在75次以上 ( 含75次 ) 為達標,試估計該年級跳繩測試達標率是多少?
(Ⅳ) 試估計這些數據的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x+2ax(a為實數),且f(1)= ![]() .
.
(1)求函數f(x)的解析式;
(2)判斷函數f(x)的奇偶性并證明;
(3)判斷函數f(x)在區間[0,+∞)的單調性,并用定義證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)═log2( ![]() +a).
+a).
(1)若f(1)<2,求實數a的取值范圍;
(2)設函數g(x)=f(x)﹣log2[(a﹣4)x+2a﹣5],討論函數g(x)的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數f(x)=Asin(ωx+φ)(ω>0,|φ|< ![]() )在某一個周期內的圖象時,列表并填入了部分數據,如表:
)在某一個周期內的圖象時,列表并填入了部分數據,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | ﹣2 | 0 |
(1)請將上表數據補充完整,并直接寫出函數f(x)的解析式;
(2)將函數y=f(x)的圖象向左平移 ![]() 個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
個單位后,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到函數y=g(x)的圖象,求g(x)的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}滿足a1+a2+…+an+2n= ![]() (an+1+1),n∈N* , 且a1=1,求證:
(an+1+1),n∈N* , 且a1=1,求證:
(1)數列{an+2n}是等比數列;
(2)求數列{an}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對一批產品的長度(單位:mm)進行抽樣檢測,下圖為檢測結果的頻率分布直方圖.根據標準,產品長度在區間[20,25)上的為一等品,在區間[15,20)和區間[25,30)上的為二等品,在區間[10,15)和[30,35)上的為三等品.用頻率估計概率,現從該批產品中隨機抽取一件,則其為二等品的概率為( ) 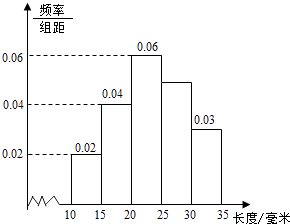
A.0.09
B.0.20
C.0.25
D.0.45
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com