
| A. | (-$\frac{1}{2}$,$\frac{3}{2}$) | B. | [-$\frac{1}{2}$,$\frac{3}{2}$] | C. | (-$\frac{3}{2}$,$\frac{1}{2}$) | D. | [-$\frac{3}{2}$,$\frac{1}{2}$] |
分析 根據(jù)新定義的運算法則化簡,轉化為二次函數(shù),分離參數(shù)求解.
解答 解:由題意:新定義x?y=x(1-y),那么:(x-a)?(x+a)=(x-a)(1-x-a)
∵不等式(x-a)?(x+a)<1對于任意實數(shù)x均成立,即(x-a)(1-x-a)<1對任意實數(shù)x均成立,
化簡得:x2-x>a2-a-1.
∵(x2-x)min=$-\frac{1}{4}$,
∴只需a2-a-1≤-$\frac{1}{4}$即可.
解得:$-\frac{1}{2}≤a≤\frac{3}{2}$,
所以a的取值范圍為[-$\frac{1}{2}$,$\frac{3}{2}$].
故選B.
點評 本題考查了新定義的運算法則,看懂運算法則的關系,轉化為熟悉的函數(shù)求解.屬于中檔題.


科目:高中數(shù)學 來源: 題型:選擇題
| A. | 4、8 | B. | 3、9 | C. | 2、10 | D. | 1、11 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | 6 | C. | -6 | D. | $-\frac{2}{3}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | a=18 B=$\frac{π}{6}$ A=$\frac{2π}{3}$ | B. | a=60 c=48 C=$\frac{2π}{3}$ | ||
| C. | a=3 b=6 A=$\frac{π}{6}$ | D. | a=14 b=15 A=$\frac{π}{4}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | [${\frac{1}{2}$,2) | B. | [1,4] | C. | [${\frac{1}{4}$,4) | D. | [${\frac{1}{2}$,4) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
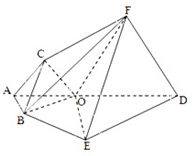 如圖,ABCDEF為多面體,平面ABED與平面ACFD垂直,點O在線段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如圖,ABCDEF為多面體,平面ABED與平面ACFD垂直,點O在線段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com