【題目】圓O1和圓O2的極坐標方程分別為ρ＝4cosθ，ρ＝－4sinθ
（1）把圓O1和圓O2的極坐標方程化為直角坐標方程；
（2）求經過圓O1、圓O2交點的直線的直角坐標方程
【答案】
（1）
【解答】以極點為原點、極軸為x軸正半軸建立平面直角坐標系，兩坐標系中取相同的長度單位．
x＝ρcosθ，y＝ρsinθ，由ρ＝4cosθ得ρ2＝4ρcosθ，
所以x2＋y2＝4x、即圓O1的直角坐標方程為x2＋y2－4x＝0，
同理圓O2的直角坐標方程為x2＋y2＋4y＝0
（2）
解：以極點為原點、極軸為x軸正半軸建立平面直角坐標系，兩坐標系中取相同的長度單位．
由 
解得 
或者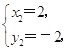 
即圓O1、圓O2交于點(0，0)和(2，－2)，故過交點的直線的直角坐標方程為y＝－x
【解析】本題主要考查了圓的極坐標方程，解決問題的關鍵是將所給極坐標方程轉化為普通方程分析計算即可
【考點精析】本題主要考查了圓的參數方程的相關知識點，需要掌握圓
的參數方程可表示為
才能正確解答此題．
開心練習課課練與單元檢測系列答案
開心試卷期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）為奇函數，當x≥0時，f（x）= 
．g（x）= 
，
（1）求當x＜0時，函數f（x）的解析式，并在給定直角坐標系內畫出f（x）在區間[﹣5，5]上的圖象；（不用列表描點） 
（2）根據已知條件直接寫出g（x）的解析式，并說明g（x）的奇偶性．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如果函數f（x）對其定義域內的兩個實數x1、x2 ， 都滿足不等式 
，則稱函數f（x）在其定義域內具有性質M．給出下列函數：① 
；②y=x2；③y=2x；④y=log2x．其中具有性質M的是（ ）
A.①④
B.②③
C.③④
D.①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某籃球隊對籃球運動員的籃球技能進行統計研究，針對籃球運動員在投籃命中時，運動員到籃筐中心的水平距離這項指標，對某運動員進行了若干場次的統計，依據統計結果繪制如下頻率分布直方圖：
(I)依據頻率分布直方圖估算該運動員投籃命中時，他到籃筐中心的水平距離的中位數；
(II)在某場比賽中，考察他前4次投籃命中時到籃筐中心的水平距離的情況，并且規定：運動員投籃命中時，他到籃筐中心的水平距離不少于4米的記1分，否則扣掉1分.用隨機變量X表示第4次投籃后的總分，將頻率視為概率，求X的分布列和均值.
查看答案和解析>>
科目：高中數學 來源： 題型：
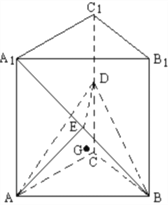
【題目】如圖，在直三棱柱
中，底面是等腰直角三角形， 
，側棱
，D、E分別是
與
的中點，點E在平面ABD上的射影是
的重心
(Ⅰ)求
與平面ABD所成角的余弦值
(Ⅱ)求點
到平面
的距離
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
﹣ax+b，在點M（1，f（1））處的切線方程為9x+3y﹣10=0，求
（1）實數a，b的值；
（2）函數f（x）的單調區間以及在區間[0，3]上的最值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
