【題目】已知函數f（x）= 
﹣ax+b，在點M（1，f（1））處的切線方程為9x+3y﹣10=0，求
（1）實數a，b的值；
（2）函數f（x）的單調區間以及在區間[0，3]上的最值．
【答案】
（1）解：因為在點M（1，f（1））處的切線方程為9x+3y﹣10=0，
所以切線斜率是k=﹣3
且9×1+3f（1）﹣10=0，
求得 
，即點 
又函數 
，則f′（x）=x2﹣a
所以依題意得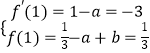 
解得 
（2）解：由（1）知 
所以f′（x）=x2﹣4=（x+2）（x﹣2）
令f′（x）=0，解得x=2或x=﹣2
當f′（x）＞0x＞2或x＜﹣2；當f′（x）＜0﹣2＜x＜2
所以函數f（x）的單調遞增區間是（﹣∞，2），（2，+∞）
單調遞減區間是（﹣2，2）
又x∈[0，3]
所以當x變化時，f（x）和f′（x）變化情況如下表：
X | 0 | （0，2） | 2 | （2，3） | 3 |
f′（x） | ﹣ | 0 | + | 0 | |
f（x） | 4 | ↘ | 極小值 | ↗ | 1 |
所以當x∈[0，3]時，f（x）max=f（0）=4，
【解析】（1）求出曲線的斜率，切點坐標，求出函數的導數，利用導函數值域斜率的關系，即可求出a，b．（2）求出導函數的符號，判斷函數的單調性以及求解閉區間的函數的最值．
【考點精析】利用利用導數研究函數的單調性和函數的最大(小)值與導數對題目進行判斷即可得到答案，需要熟知一般的,函數的單調性與其導數的正負有如下關系： 在某個區間
內，(1)如果
，那么函數
在這個區間單調遞增；(2)如果
，那么函數
在這個區間單調遞減；求函數在
上的最大值與最小值的步驟：（1）求函數在內的極值；（2）將函數的各極值與端點處的函數值
，
比較，其中最大的是一個最大值，最小的是最小值．
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=loga（1+x），g（x）=loga（1﹣x），其中（a＞0且a≠1），設h（x）=f（x）﹣g（x）．
（1）求h（x）的定義域；
（2）判斷h（x）的奇偶性，并說明理由；
（3）若a=log327+log2，求使f（x）＞1成立的x的集合．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是定義在[﹣1，1]上的奇函數，且f（1）=1，若對任意m，n∈[﹣1，1]，m+n≠0，都有 
．
（1）用定義證明函數f（x）在定義域上是增函數；
（2）若 
，求實數a的取值范圍；
（3）若不等式f（x）≤（1﹣2a）t+2對所有和x∈[﹣1，1]，a∈[﹣1，1]都恒成立，求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圓O1和圓O2的極坐標方程分別為ρ＝4cosθ，ρ＝－4sinθ
（1）把圓O1和圓O2的極坐標方程化為直角坐標方程；
（2）求經過圓O1、圓O2交點的直線的直角坐標方程
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
在圓
上， 
的坐標分別為
， 
，線段
的垂直平分線交線段
于點
（1）求點
的軌跡
的方程；
（2）設圓
與點
的軌跡
交于不同的四個點
，求四邊形
的面積的最大值及相應的四個點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某產品的三個質量指標分別為x，y，z，用綜合指標S=x+y+z評價該產品的等級．若S≤4，則該產品為一等品．現從一批該產品中，隨機抽取10件產品作為樣本，其質量指標列表如下：
產品編號 | A1 | A2 | A3 | A4 | A5 |
質量指標 | （1，1，2） | （2，1，1） | （2，2，2） | （1，1，1） | （1，2，1） |
產品編號 | A6 | A7 | A8 | A9 | A10 |
質量指標 | （1，2，2） | （2，1，1） | （2，2，1） | （1，1，1） | （2，1，2） |
（1）利用上表提供的樣本數據估計該批產品的一等品率．
（2）在該樣品的一等品中，隨機抽取2件產品， ①用產品編號列出所有可能的結果；
②設事件B為“在取出的2件產品中，每件產品的綜合指標S都等于4”，求事件B發生的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數y=f（x）的定義域是[0，4]，則函數g（x）= 
的定義域是（ ）
A.[0，2]
B.[0，2）
C.[0，1）∪（1，2]
D.[0，4]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一列火車從重慶駛往北京，沿途有n個車站（包括起點站重慶和終點站北京）．車上有一郵政車廂，每停靠一站便要卸下火車已經過的各站發往該站的郵袋各1個，同時又要裝上該站發往以后各站的郵袋各1個，設從第k站出發時，郵政車廂內共有郵袋ak個（k=1，2，…，n）．
（1）求數列{ak}的通項公式；
（2）當k為何值時，ak的值最大，求出ak的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
