
【題目】一列火車從重慶駛往北京,沿途有n個車站(包括起點站重慶和終點站北京).車上有一郵政車廂,每停靠一站便要卸下火車已經過的各站發往該站的郵袋各1個,同時又要裝上該站發往以后各站的郵袋各1個,設從第k站出發時,郵政車廂內共有郵袋ak個(k=1,2,…,n).
(1)求數列{ak}的通項公式;
(2)當k為何值時,ak的值最大,求出ak的最大值.
科目:高中數學 來源: 題型:
【題目】某廠用鮮牛奶在某臺設備上生產A,B兩種奶制品.生產1噸A產品需鮮牛奶2噸,使用設備1小時,獲利1 000元;生產1噸B產品需鮮牛奶1.5噸,使用設備1.5小時,獲利1 200元.要求每天B產品的產量不超過A產品產量的2倍,設備每天生產A,B兩種產品時間之和不超過12小時.假定每天可獲取的鮮牛奶數量W(單位:噸)是一個隨機變量,其分布列為
W | 12 | 15 | 18 |
P | 0.3 | 0.5 | 0.2 |
該廠每天根據獲取的鮮牛奶數量安排生產,使其獲利最大,因此每天的最大獲利Z(單位:元)是一個隨機變量.
(I)求Z的分布列和均值;
(II)若每天可獲取的鮮牛奶數量相互獨立,求3天中至少有1天的最大獲利超過10 000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的外接圓半徑
的外接圓半徑![]() ,角A、B、C的對邊分別是a、b、c,且
,角A、B、C的對邊分別是a、b、c,且![]() .
.
(I)求角B和邊長b;
(II)求![]() 面積的最大值及取得最大值時的a、c的值,并判斷此時三角形的形狀.
面積的最大值及取得最大值時的a、c的值,并判斷此時三角形的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫療研究所為了檢驗某種血清預防感冒的作用,把500名使用血清的人與另外500名未使用血清的人一年中的感冒記錄作比較,提出假設H:“這種血清不能起到預防感冒的作用”,利用2×2列聯表計算的K2≈3.918,經查臨界值表知P(K2≥3.841)≈0.05.則下列表述中正確的是( )
A.有95℅的把握認為“這種血清能起到預防感冒的作用”
B.若有人未使用該血清,那么他一年中有95℅的可能性得感冒
C.這種血清預防感冒的有效率為95℅
D.這種血清預防感冒的有效率為5℅
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,A , B , C是三個觀察站,A在B的正東,兩地相距6km,C在B的北偏西30°,兩地相距4km,在某一時刻,A觀察站發現某種信號,并知道該信號的傳播速度為1km/s,4s后B , C兩個觀察站同時發現這種信號,在以過A , B兩點的直線為x軸,以AB的垂直平分線為y軸建立的平面直角坐標系中,指出發出這種信號的P的坐標.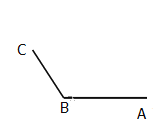
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PD垂直于底面ABCD,AD=PD,E分別為AP的中點.
(Ⅰ)求證:DE垂直于平面PAB;
(Ⅱ)設BC =![]() ,AB=2,求直線EB與平面ABD所成的角的大小.
,AB=2,求直線EB與平面ABD所成的角的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,直線l的參數方程為 (t為參數).在以原點O為極點,x軸正半軸為極軸的極坐標系中,圓C的方程為ρ=4cosθ.
(t為參數).在以原點O為極點,x軸正半軸為極軸的極坐標系中,圓C的方程為ρ=4cosθ.
(1)寫出直線l的普通方程和圓C的直角坐標方程.
(2)若點P坐標為(1,1),圓C與直線l交于A,B兩點,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知下列四個命題:
①函數f(x)= ![]() x﹣lnx(x>0),則y=f(x)在區間(
x﹣lnx(x>0),則y=f(x)在區間( ![]() ,1)內無零點,在區間(1,e)內有零點;
,1)內無零點,在區間(1,e)內有零點;
②函數f(x)=log2(x+ ![]() ),g(x)=1+
),g(x)=1+ ![]() 不都是奇函數;
不都是奇函數;
③若函數f(x)滿足f(x﹣1)=﹣f(x+1),且f(1)=2,則f(7)=﹣2;
④設x1、x2是關于x的方程|logax|=k(a>0且a≠1)的兩根,則x1x2=1,
其中正確命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法不正確的是
A.命題“對![]() ,都有
,都有![]() ”的否定為“
”的否定為“![]() ,使得
,使得![]() ”
”
B.“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
C. “若![]() ,則
,則![]() ” 是真命題
” 是真命題
D.甲、乙兩位學生參與數學模擬考試,設命題![]() 是“甲考試及格”,
是“甲考試及格”,![]() 是“乙考試及格”,則命題“至少有一位學生不及格”可表示為
是“乙考試及格”,則命題“至少有一位學生不及格”可表示為![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com