
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PD垂直于底面ABCD,AD=PD,E分別為AP的中點.
(Ⅰ)求證:DE垂直于平面PAB;
(Ⅱ)設BC =![]() ,AB=2,求直線EB與平面ABD所成的角的大小.
,AB=2,求直線EB與平面ABD所成的角的大小.

【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)易證得DE⊥AP及AB⊥DE,進而可證得DE垂直于平面PAB;
(2)在面APD內,過E做EH⊥AD交AD于H,連接BH,∠EBH就是直線EB與平面ABD所成的角,進而可得解.
試題解析:
(1)∵PD垂直于底面ABCD
∴AB⊥PD
又∵底面ABCD為矩形
∴AB⊥AD
∴AB⊥APD
∵DE![]() 面APD
面APD
∴AB⊥DE
又∵E為AP的中點,AD=PD
∴DE⊥AP
∴DE垂直于平面PAB
(2)在面APD內,過E做EH⊥AD交AD于H,連接BH,∠EBH就是直線EB與平面ABD所成的角
∵BC =![]() ,AB=2,AD=PD,E為AP的中點
,AB=2,AD=PD,E為AP的中點
∴BE=![]() ,EH=
,EH=![]()
∴sin∠EBH=![]()


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,其中a>0,且函數f(x)的最大值是
,其中a>0,且函數f(x)的最大值是 ![]()
(1)求實數a的值;
(2)若函數g(x)=lnf(x)﹣b有兩個零點,求實數b的取值范圍;
(3)若對任意的x∈(0,2),都有f(x)< ![]() 成立,求實數k的取值范圍.
成立,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)= ![]() (a∈R)是奇函數,函數g(x)=
(a∈R)是奇函數,函數g(x)= ![]() 的定義域為(﹣1,+∞).
的定義域為(﹣1,+∞).
(1)求a的值;
(2)若g(x)= ![]() 在(﹣1,+∞)上遞減,根據單調性的定義求實數m的取值范圍;
在(﹣1,+∞)上遞減,根據單調性的定義求實數m的取值范圍;
(3)在(2)的條件下,若函數h(x)=f(x)+g(x)在區間(﹣1,1)上有且僅有兩個不同的零點,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一列火車從重慶駛往北京,沿途有n個車站(包括起點站重慶和終點站北京).車上有一郵政車廂,每停靠一站便要卸下火車已經過的各站發往該站的郵袋各1個,同時又要裝上該站發往以后各站的郵袋各1個,設從第k站出發時,郵政車廂內共有郵袋ak個(k=1,2,…,n).
(1)求數列{ak}的通項公式;
(2)當k為何值時,ak的值最大,求出ak的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)為奇函數,當x≥0時,f(x)= ![]() .g(x)=
.g(x)= ![]() ,
,
(1)求當x<0時,函數f(x)的解析式;
(2)求g(x)的解析式,并證明g(x)的奇偶性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如圖.
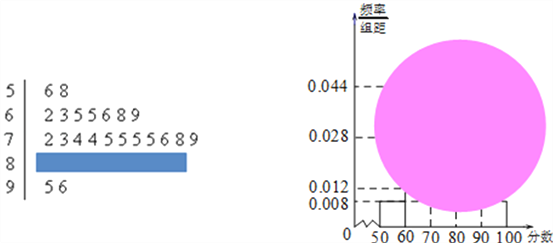
(Ⅰ)求分數在[50,60)的頻率及全班人數;
(Ⅱ)求分數在[80,90)之間的頻數,并計算頻率分布直方圖中[80,90)間矩形的高;
(Ⅲ)若要從分數在[80,100)之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在[90,100)之間的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com