
【題目】如圖,菱形ABCD的對角線AC與BD交于點O,點E,F分別在AD,CD上,AE=CF,EF交BD于點H.將△DEF沿EF折到△D′EF的位置.
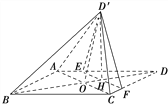
(1)證明:AC⊥HD′;
(2)若AB=5,AC=6,AE=![]() ,OD′=2
,OD′=2![]() ,求五棱錐D′ABCFE的體積.
,求五棱錐D′ABCFE的體積.
【答案】(1)詳見解析(2)![]()
【解析】試題分析:(1)折疊后仍有EF⊥HD,而AC∥EF,可得AC⊥HD′.(2)先定高線:OD′,由勾股定理得OD′⊥OH.由(1)得AC⊥OD′.因此OD′⊥平面ABC.再根據錐體體積公式求體積
試題解析:(1)證明:由已知得AC⊥BD,AD=CD.
又由AE=CF得![]() =
=![]() ,故AC∥EF.
,故AC∥EF.
由此得EF⊥HD,故EF⊥HD′,所以AC⊥HD′.
(2)由EF∥AC得![]() .
.
由AB=5,AC=6得DO=BO=![]() =4.
=4.
所以OH=1,D′H=DH=3.
于是OD′2+OH2=(2![]() )2+12=9=D′H2,
)2+12=9=D′H2,
故OD′⊥OH.
由(1)知AC⊥HD′,又AC⊥BD,BD∩HD′=H,
所以AC⊥平面BHD′,于是AC⊥OD′.
又由OD′⊥OH,AC∩OH=O,所以OD′⊥平面ABC.
又由![]() =
=![]() 得EF=
得EF=![]() .
.
五邊形ABCFE的面積S=![]() ×6×8-
×6×8-![]() ×
×![]() ×3=
×3=![]() .
.
所以五棱錐D′ABCFE的體積V=![]() ×
×![]() ×2
×2![]() =
=![]() .
.
點睛:立體幾何中折疊問題,要注重折疊前后垂直關系的變化,不變的垂直關系是解決問題的關鍵條件.


科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著機構改革工作的深入進行,各單位要減員增效,有一家公司現有職員2a人(140<2a<420,且a為偶數),每人每年可創利b萬元.據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利0.01b萬元,但公司需付下崗職員每人每年0.4b萬元的生活費,并且該公司正常運轉所需人數不得小于現有職員的![]() ,為獲得最大的經濟效益,該公司應裁員多少人?
,為獲得最大的經濟效益,該公司應裁員多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,直線
,直線![]() 與圓
與圓![]() 相切.
相切.
(1)求橢圓的方程;
(2)已知定點![]() ,若直線
,若直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點,試判斷是否存在實數
兩點,試判斷是否存在實數![]() ,使得以
,使得以![]() 為直徑的圓過定點
為直徑的圓過定點![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人參加了一家公司的招聘面試,面試合格者可正式簽約,甲表示只要面試合格就簽約.乙、丙則約定:兩人面試都合格就一同簽約,否則兩人都不簽約.設甲、乙、丙面試合格的概率分別是![]() ,
, ![]() ,
, ![]() ,且面試是否合格互不影響.求:
,且面試是否合格互不影響.求:
(1)至少有1人面試合格的概率;
(2)簽約人數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com