
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)函數![]() 在
在![]() 上的最大值
上的最大值![]() .
.
①求![]() ;
;
②若過點![]() 可作出曲線
可作出曲線![]() 的三條切線,求
的三條切線,求![]() 的范圍.
的范圍.
【答案】(1)見解析;(2)①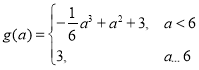 ;②
;②![]() 或
或![]() 且
且![]() .
.
【解析】
(1)求![]() ,令
,令![]() 便得到
便得到![]() ,或
,或![]() ,所以討論
,所以討論![]() 和2的關系,即判斷
和2的關系,即判斷![]() 和0的關系:分
和0的關系:分![]() ,
,![]() ,
,![]() 三種情況,判斷每種情況下的
三種情況,判斷每種情況下的![]() 的符號,從而判斷
的符號,從而判斷![]() 的單調性;
的單調性;
(2)①對應(1)中的三種情況:![]() ,
,![]() ,
,![]() ,判斷在每種情況下
,判斷在每種情況下![]() 在
在![]() ,
,![]() 上的單調性,根據單調性求函數
上的單調性,根據單調性求函數![]() 在
在![]() ,
,![]() 上的最大值
上的最大值![]() ;
;
②要作![]() 的三條切線,則
的三條切線,則![]() 圖象應是曲線,所以
圖象應是曲線,所以![]() ,
,![]() ,求
,求![]() ,設切點為
,設切點為![]() ,將切點
,將切點![]() 代入切線方程,則這個關于
代入切線方程,則這個關于![]() 的方程有三個不同的實數根,再利用導數研究三次方程根的情況,即可求得
的方程有三個不同的實數根,再利用導數研究三次方程根的情況,即可求得![]() 的取值范圍.
的取值范圍.
(1)![]() ,令
,令![]() 得,
得,![]() ,或
,或![]() ;
;
若![]() ,即
,即![]() ,
,
![]() ,或
,或![]() 時,
時,![]() ;
;![]() 時,
時,![]() ;
;
![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() ,
,![]() 上單調遞減;
上單調遞減;
若![]() ,即
,即![]() ,
,![]() ,
,
![]() 函數
函數![]() 在
在![]() 上單調遞增;
上單調遞增;
若![]() ,
,![]() ,
,![]() ,或
,或![]() 時,
時,![]() ;
;![]() 時,
時,![]() ;
;
![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 單調遞減;
單調遞減;
(2)①由(1)知:
![]() 當
當![]() 時,
時,![]() 在
在![]() ,
,![]() 單調遞減,在
單調遞減,在![]() ,
,![]() 單調遞增;
單調遞增;
![]() 對于此時的
對于此時的![]() 的最大值比較
的最大值比較![]() ,
,![]() 即可;
即可;
∵![]() ,
,
![]() 時,
時,![]() ,∴
,∴![]() ;
;
∵![]() 時,
時,![]() ,∴
,∴![]() ;
;
![]() 當
當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增,∴
上單調遞增,∴![]() ;
;
![]() 當
當![]() 時,
時,![]() 在
在![]() ,
,![]() 上單調遞增,∴
上單調遞增,∴![]() ;
;
∴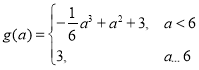 ;
;
②根據題意,![]() ,
,![]() ,
,
所以設過點![]() 所作切線的切點為
所作切線的切點為![]() ,
,![]() ,斜率為
,斜率為![]() ;
;
![]() 切線方程為
切線方程為![]() ,
,
∵點![]() 在切線上,所以
在切線上,所以![]() ,
,
將上式整理成:![]() ,
,
則關于![]() 的方程有三個不同的實數根,且
的方程有三個不同的實數根,且![]() ;
;
令![]() ,
,
則![]() 應有三個不同的零點,
應有三個不同的零點,![]() ,令
,令![]() ,則
,則![]() ,或
,或![]() ,
,![]() ,
,![]() 中一個是極大值,一個是極小值;
中一個是極大值,一個是極小值;
![]() 時,
時,![]() 是極小值,
是極小值,![]() 是極大值,
是極大值,![]()
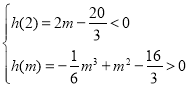 ;
;
解![]() 得
得![]() ;
;
令![]() ,
,![]() ,令
,令![]() ,得,
,得,![]() ,或4;
,或4;
![]() 在
在![]() ,
,![]() 上單調遞減,在
上單調遞減,在![]() ,
,![]() 上單調遞增;
上單調遞增;
可求得![]() ,
,![]() ,時,
,時,![]() ,
,![]() ,且
,且![]() 時,
時,![]() ;
;
![]() 的解是
的解是![]() ,
,![]() ;
;
![]() 時,
時,![]() 是極大值,
是極大值,![]() 是極小值,
是極小值,![]()
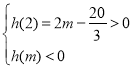 ;
;
解![]() 得,
得,![]() ;
;
∴![]() 的解是
的解是![]() ,且
,且![]() ,
,![]() ,且
,且![]() ;
;
綜上得![]() 的取值范圍是
的取值范圍是![]() 或
或![]() 且
且![]() .
.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,過橢圓
,過橢圓![]() 的左焦點和上頂點的直線與圓
的左焦點和上頂點的直線與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 與原點
與原點![]() 關于直線
關于直線![]() 對稱,試求四邊形
對稱,試求四邊形![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別是a,b,c,且csin2B﹣bsin(A+B)=0
(1)求角B的大小;
(2)設a=4,c=6,求sinC的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】把函數![]() 的圖象沿
的圖象沿![]() 軸向左平移
軸向左平移![]() 個單位,縱坐標伸長到原來的2倍(橫坐標不變)后得到函數
個單位,縱坐標伸長到原來的2倍(橫坐標不變)后得到函數![]() 的圖象,對于函數
的圖象,對于函數![]() 有以下四個判斷:
有以下四個判斷:
①該函數的解析式為;![]() ;
;
②該函數圖象關于點![]() 對稱;
對稱;
③該函數在![]() [,上是增函數;
[,上是增函數;
④函數![]() 在
在![]() 上的最小值為
上的最小值為![]() ,則
,則![]() .
.
其中,正確判斷的序號是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 、
、![]() 、
、![]() ,對于給定的正整數
,對于給定的正整數![]() ,記
,記![]() ,
,![]()
![]() .若對任意的正整數
.若對任意的正整數![]() 滿足:
滿足:![]() ,且
,且![]() 是等差數列,則稱數列
是等差數列,則稱數列![]() 為“
為“![]() ”數列.
”數列.
(1)若數列![]() 的前
的前![]() 項和為
項和為![]() ,證明:
,證明:![]() 為
為![]() 數列;
數列;
(2)若數列![]() 為
為![]() 數列,且
數列,且![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(3)若數列![]() 為
為![]() 數列,證明:
數列,證明:![]() 是等差數列 .
是等差數列 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】南北朝時代的偉大科學家祖暅在數學上有突出貢獻,他在實踐的基礎上提出祖暅原理:“冪勢既同,則積不容異”. 其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平行平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等.如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面面積分別為![]() ,則“
,則“![]() 相等”是“
相等”是“![]() 總相等”的
總相等”的
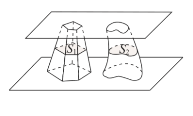
A. 充分而不必要條件B. 必要而不充分條件
C. 充分必要條件D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 的前
的前![]() 項和為
項和為![]() ,記
,記![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,且數列
,且數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)① 計算![]() ,
,![]() 的值;
的值;
② 猜想![]() ,
,![]() 滿足的關系式,并用數學歸納法加以證明;
滿足的關系式,并用數學歸納法加以證明;
(2)若數列![]() 通項公式為
通項公式為![]() ,證明:
,證明:![]() .
.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com