
已知a、b、c分別是△ABC三個內角A、B、C的對邊.
(1)若△ABC面積為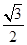 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;
(2)若acosA=bcosB,試判斷△ABC的形狀,證明你的結論.
(1)a= ,b=1,(2)直角三角形或等腰三角形
,b=1,(2)直角三角形或等腰三角形
解析試題分析:(1)解三角形問題,一般利用正余弦定理進行邊角轉化.由面積公式有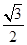 =
= bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a=
bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a= .(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B為三角形內角,∴A+B=90º或A=B.∴△ABC為直角三角形或等腰三角形.本題也可從余弦定理出發:
.(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B為三角形內角,∴A+B=90º或A=B.∴△ABC為直角三角形或等腰三角形.本題也可從余弦定理出發: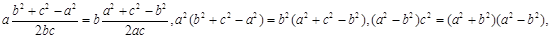 所以
所以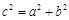 或
或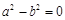 .
.
解:(1)由已知得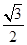 =
= bcsinA=bsin60º,∴b=1.
bcsinA=bsin60º,∴b=1.
由余弦定理a2=b2+c2-2bccosA=3,∴a= .
.
(2)由正弦定理得2RsinA=a,2RsinB=b,
∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B為三角形內角,
∴A+B=90º或A=B.∴△ABC為直角三角形或等腰三角形
考點:正余弦定理


科目:高中數學 來源: 題型:解答題
已知角A、B、C為△ABC的三個內角,其對邊分別為a、b、c,若 =(-cos
=(-cos ,sin
,sin ),
), =(cos
=(cos ,sin
,sin ),a=2
),a=2 ,且
,且 ·
· =
= .
.
(1)若△ABC的面積S= ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com