
分析 (1)根據數量積公式化簡$\overrightarrow{m}•\overrightarrow{n}$,利用正弦函數的性質得出A的值;
(2)利用二倍角公式化簡,根據二次函數的性質和sinx的范圍求出最值.
解答 解:(1)由題已知:∵$m•n=\sqrt{3}sinA+cosA=\sqrt{3}$,
∴$2sin(A+\frac{π}{6})=\sqrt{3}$,$sin(A+\frac{π}{6})=\frac{{\sqrt{3}}}{2}$.
由A為銳角得:$A+\frac{π}{6}=\frac{π}{3}$,$A=\frac{π}{6}$.
(2)由(Ⅰ)知$sinA=\frac{1}{2}$,
∴f(x)=cos2x+2sinx=1-2sin2x+2sinx=$-2{(sinx-\frac{1}{2})^2}+\frac{3}{2}$,
∵x∈R,∴sinx∈[-1,1],
∴當sinx=$\frac{1}{2}$時,f(x)有最大值$\frac{3}{2}$,
當sinx=-1時,f(x)有最小值-3,
故所求函數f(x)的值域是$[-3,\;\frac{3}{2}]$.
點評 本題考查了平面向量的數量積運算,三角函數的恒等變換,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (e,e2) | B. | (1,e2) | C. | $(\frac{1}{e},e)$ | D. | $(\frac{1}{e},{e^2})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
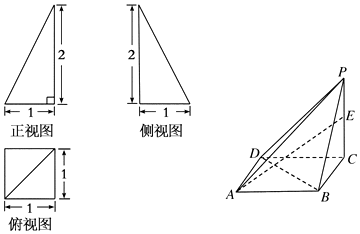
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 0 | C. | -$\frac{1}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,則$\overrightarrow{b}$=$\overrightarrow{c}$, | B. | 若$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,則|$\overrightarrow{a}$|+|$\overrightarrow{b}$|>|$\overrightarrow{c}$| | ||
| C. | 若($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=0,則$\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$•$\overrightarrow{b}$>0,則向量$\overrightarrow{a}$,$\overrightarrow{b}$的夾角為銳角 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com