【題目】函數f（x）是定義在R上的偶函數，且滿足f（x+2）=f（x）．當x∈[0，1]時，f（x）=2x．若在區間[﹣2，3]上方程ax+2a﹣f（x）=0恰有四個不相等的實數根，則實數a的取值范圍是（ ）
A.（ 
， 
）
B.（ ， 
）
C.（ ，2）
D.（1，2）
【答案】A
【解析】解：若在區間[﹣2，3]上方程ax+2a﹣f（x）=0恰有四個不相等的實數根，等價為f（x）=a（x+2）有四個不相等的實數根，
即函數y=f（x）和g（x）=a（x+2），有四個不相同的交點，
∵f（x+2）=f（x），∴函數的周期是2，
當﹣1≤x≤0時，0≤﹣x≤1，此時f（﹣x）=﹣2x，
∵f（x）是定義在R上的偶函數，
∴f（﹣x）=﹣2x=f（x），
即f（x）=﹣2x，﹣1≤x≤0，
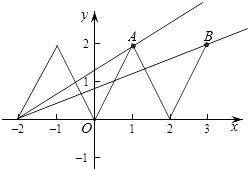
作出函數f（x）和g（x）的圖象，
當g（x）經過A（1，2）時，兩個圖象有3個交點，此時g（1）=3a=2，解得a= 
當g（x）經過B（3，2）時，兩個圖象有5個交點，此時g（3）=5a=2，解得a= 
，
要使在區間[﹣2，3]上方程ax+2a﹣f（x）=0恰有四個不相等的實數根，
則 
，
故選：A
時刻準備著暑假作業原子能出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，正方形
的邊長為
，已知
，將
沿
邊折起，折起后
點在平面
上的射影為
點，則翻折后的幾何體中有如下描述：①
與
所成角的正切值為
；②
；③
；④平面
平面
，其中正確的命題序號為___________．
查看答案和解析>>
科目：高中數學 來源： 題型：
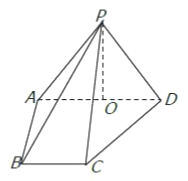
【題目】如圖，在四棱錐
中，側面
底面
，側棱
，底面
為直角梯形，其中
為
中點.
（1）求證： 
平面
；
（2）求異面直線
與
所成角的余弦值；
（3）線段
上是否存在
，使得它到平面
的距離為
？若存在，求出
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分16分）某批發公司批發某商品，每件商品進價80元，批發價120元，該批發商為鼓勵經銷商批發，決定當一次批發量超過100個時，每多批發一個，批發的全部商品的單價就降低0．04元，但最低批發價不能低于102元．
（1）當一次訂購量為多少個時,每件商品的實際批發價為102元?
（2）當一次訂購量為
個, 每件商品的實際批發價為
元,寫出函數
的表達式；
（3）根據市場調查發現,經銷商一次最大定購量為
個，則當經銷商一次批發多少個零件時,該批發公司可獲得最大利潤．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市在發展過程中，交通狀況逐漸受到有關部門的關注，據有關統計數據顯示，從上午6點到中午12點，車輛通過該市某一路段的用時y（分鐘）與車輛進入該路段的時刻t之間的關系可近似地用如下函數給出： y=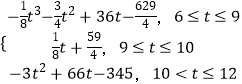 
求從上午6點到中午12點，通過該路段用時最多的時刻．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=alnx﹣4x，g（x）=﹣x2﹣3． （Ⅰ）求函數f（x）在x=1處的切線方程；
（Ⅱ）若存在x0∈[e，e2]，使得f（x0）＜g（x0）成立，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
