
分析 (1)當n=1時,a1=S1,由條件求得首項,根據an+1=Sn+1-Sn,求得an+1+1=2(an+1),判斷出數列{an+1}是等比數列;
(2)利用等比數列的通項公式求得an+1,進而求得an;
(3)設存在k,k+1,k+2∈N*,使得ak,ak+1,ak+2成等差數列,根據等差中項的性質,化簡整理,結合指數函數的值域,即可判斷存在性.
解答 解:(1)證明:因為Sn=2an-n,
當n=1時,a1=S1=2a1-1,解得a1=1,
因為Sn=2an-n,
所以Sn+1=2an+1-(n+1),
則an+1=2an+1-2an-1,
所以an+1=2an+1,
所以an+1+1=2(an+1)
數列{an+1}是首項和公比均為2的等比數列;
(2)由(1)知,數列{an+1}是等比數列,
所以an+1=2•2n-1=2n,
所以an=2n-1.
(3)假設存在k,k+1,k+2∈N*,使得ak,ak+1,ak+2成等差數列,
則2ak+1=ak+ak+2,即2(2k+1-1)=2k-1+2k+2-1,
即2k+2=2k+2k+2,即有2k=0,這與2k>0矛盾,
故數列{an}中不存在連續三項可以構成等差數列.
點評 本題考查數列的通項公式的求法,探索數列{an}中是否存在連續三項成等差數列,注意構造法和轉化思想的運用,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
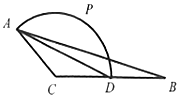 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中點.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | {x|x≠±2} | D. | (-2,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
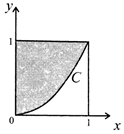 在如圖所示的正方形中隨機投擲10000個點,則落入陰影部分(曲線C的方程為x2-y=0)的點的個數的估計值為( )
在如圖所示的正方形中隨機投擲10000個點,則落入陰影部分(曲線C的方程為x2-y=0)的點的個數的估計值為( )| A. | 5000 | B. | 6667 | C. | 7500 | D. | 7854 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [1,2] | B. | (1,2) | C. | (-2,-1) | D. | [-2,-1] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com