
| A. | $\frac{2}{3}$ | B. | $\frac{11}{27}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{27}$ |
分析 根據條件求出函數有零點的取值范圍,利用幾何概型的概率公式,求出相應的面積即可得到結論.
解答 解:若函數f(x)在R上有零點,
則滿足判別式△=4b-4a2≥0,即b>a2
區域$\left\{\begin{array}{l}x+y-6≤0\\ x>0\\ y>0\end{array}$的面積S=$\frac{1}{2}×6×6$=18,
由$\left\{\begin{array}{l}{y={x}^{2}}\\{x+y-6=0}\end{array}\right.$,解得x=2,y=4,即(2,4),
則函數f(x)在R上有零點,區域的面積S=${∫}_{0}^{2}(6-x-{x}^{2})dx$=$(6x-\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}){|}_{0}^{2}$=$\frac{22}{3}$,
∴根據幾何概型的概率公式可知函數f(x)在R上有零點的概率為$\frac{11}{27}$,
故選:B.
點評 本題主要考查幾何概型的概率計算,以及利用積分求區域面積,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
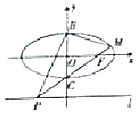 如圖,已知橢圓$\frac{x^2}{a^2}+{y^2}=1(a>1)$的長軸長是短軸長的2倍,右焦點為F,點B,C分別是該橢圓的上、下頂點,點P是直線l:y=-2上的一個動點(與y軸交點除外),直線PC交橢圓于另一點M,記直線BM,BP的斜率分別為k1,k2.
如圖,已知橢圓$\frac{x^2}{a^2}+{y^2}=1(a>1)$的長軸長是短軸長的2倍,右焦點為F,點B,C分別是該橢圓的上、下頂點,點P是直線l:y=-2上的一個動點(與y軸交點除外),直線PC交橢圓于另一點M,記直線BM,BP的斜率分別為k1,k2.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 88% | B. | 42% | C. | 40% | D. | 16% |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{2}$ | B. | 2 | C. | $3+2\sqrt{2}$ | D. | $4+2\sqrt{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com