
【題目】己知n為正整數,數列{an}滿足an>0,4(n+1)an2﹣nan+12=0,設數列{bn}滿足bn= ![]()
(1)求證:數列{ ![]() }為等比數列;
}為等比數列;
(2)若數列{bn}是等差數列,求實數t的值:
(3)若數列{bn}是等差數列,前n項和為Sn , 對任意的n∈N* , 均存在m∈N* , 使得8a12Sn﹣a14n2=16bm成立,求滿足條件的所有整數a1的值.
【答案】
(1)證明:數列{an}滿足an>0,4(n+1)an2﹣nan+12=0,
∴ ![]() =
= ![]() an+1,即
an+1,即 ![]() =2
=2 ![]() ,
,
∴數列{ ![]() }是以a1為首項,以2為公比的等比數列
}是以a1為首項,以2為公比的等比數列
(2)解:由(1)可得: ![]() =
= ![]() ,∴
,∴ ![]() =n
=n ![]() 4n﹣1.
4n﹣1.
∵bn= ![]() ,∴b1=
,∴b1= ![]() ,b2=
,b2= ![]() ,b3=
,b3= ![]() ,
,
∵數列{bn}是等差數列,∴2× ![]() =
= ![]() +
+ ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() ,
,
化為:16t=t2+48,解得t=12或4
(3)解:數列{bn}是等差數列,由(2)可得:t=12或4.
①t=12時,bn= ![]() =
= ![]() ,Sn=
,Sn= 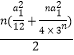 ,
,
∵對任意的n∈N*,均存在m∈N*,使得8a12Sn﹣a14n2=16bm成立,
∴8 ![]() ×
×  ﹣a14n2=16×
﹣a14n2=16× ![]() ,
,
∴ ![]()
![]() =
= ![]() ,n=1時,化為:﹣
,n=1時,化為:﹣ ![]() =
= ![]() >0,無解,舍去.
>0,無解,舍去.
②t=4時,bn= ![]() =
= ![]() ,Sn=
,Sn=  ,
,
對任意的n∈N*,均存在m∈N*,使得8a12Sn﹣a14n2=16bm成立,
∴8 ![]() ×
×  ﹣a14n2=16×
﹣a14n2=16× ![]() ,
,
∴n ![]() =4m,
=4m,
∴a1=2 ![]() .∵a1為正整數,∴
.∵a1為正整數,∴ ![]() =
= ![]() k,k∈N*.
k,k∈N*.
∴滿足條件的所有整數a1的值為{a1|a1=2 ![]() ,n∈N*,m∈N*,且
,n∈N*,m∈N*,且 ![]() =
= ![]() k,k∈N*}
k,k∈N*}
【解析】(1)數列{an}滿足an>0,4(n+1)an2﹣nan+12=0,化為: ![]() =2×
=2× ![]() ,即可證明.(2)由(1)可得:
,即可證明.(2)由(1)可得: ![]() =
= ![]() ,可得
,可得 ![]() =n
=n ![]() 4n﹣1 . 數列{bn}滿足bn=
4n﹣1 . 數列{bn}滿足bn= ![]() ,可得b1 , b2 , b3 , 利用數列{bn}是等差數列即可得出t.(3)根據(2)的結果分情況討論t的值,化簡8a12Sn﹣a14n2=16bm , 即可得出a1 .
,可得b1 , b2 , b3 , 利用數列{bn}是等差數列即可得出t.(3)根據(2)的結果分情況討論t的值,化簡8a12Sn﹣a14n2=16bm , 即可得出a1 .


科目:高中數學 來源: 題型:
【題目】某校高三年級實驗班與普通班共1000名學生,其中實驗班學生200人,普通班學生800人,現將高三一模考試數學成績制成如圖所示頻數分布直方圖,按成績依次分為5組,其中第一組([0, 30)),第二組([30, 60)),第三組([60, 90)),的頻數成等比數列,第一組與第五組([120, 150))的頻數相等,第二組與第四組([90, 120))的頻數相等。
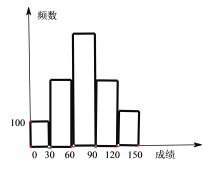
(1)求第三組的頻率;
(2)已知實驗班學生成績![]() 在第五組,
在第五組,![]() 在第四組,剩下的都在第三組,試估計實驗班學生數學成績的平均分;
在第四組,剩下的都在第三組,試估計實驗班學生數學成績的平均分;
(3)在(2)的條件下,按分層抽樣的方法從第5組中抽取5人進行經驗交流,再從這5人中隨機抽取3人在全校師生大會上作經驗報告,求抽取的3人中恰有一個普通班學生的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程![]() .
.
(![]() )若已知方程表示橢圓,則
)若已知方程表示橢圓,則![]() 的取值范圍為__________.
的取值范圍為__________.
(![]() )語句“
)語句“![]() ”是語句“方程
”是語句“方程![]() ”表示雙曲線的(_____________).
”表示雙曲線的(_____________).
A.充分不必要條件 B.必要不充分條件 C.充在條件 D.既不充分也不必要條件
(![]() )根據(
)根據(![]() )的結論,以“如果
)的結論,以“如果![]() 那么
那么![]() ”的形式寫出一個正確命題,記作命題
”的形式寫出一個正確命題,記作命題![]() ,則
,則
命題![]() :__________.
:__________.
(![]() )套用量詞命題的格式:“
)套用量詞命題的格式:“![]() ,
, ![]() ”或“
”或“![]() ,
, ![]() ”,改寫(
”,改寫(![]() )中命題
)中命題![]() ,
,
表述形式為:__________.
(![]() )寫出(
)寫出(![]() )中命題
)中命題![]() 的逆命題,記作命題
的逆命題,記作命題![]() ,則
,則
命題![]() :__________.
:__________.
(![]() )判斷(
)判斷(![]() )中命題
)中命題![]() 的真假,并陳述判斷理由.
的真假,并陳述判斷理由.
![]() 命題為__________命題,因為__________.
命題為__________命題,因為__________.
(![]() )若已知方程表示橢圓,則該橢圓兩個焦點的坐標分別為__________.
)若已知方程表示橢圓,則該橢圓兩個焦點的坐標分別為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過拋物線![]() 的焦點
的焦點![]() ,斜率為
,斜率為![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點,且
兩點,且![]() .
.
(1)求該拋物線![]() 的方程;
的方程;
(2)已知拋物線上一點![]() ,過點
,過點![]() 作拋物線的兩條弦
作拋物線的兩條弦![]() 和
和![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?并說明理由.
是否過定點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數f(x)=4sin(2x+![]() ), (x∈R)有下列命題:
), (x∈R)有下列命題:
①y=f(x)是以2π為最小正周期的周期函數;
② y=f(x)可改寫為y=4cos(2x-![]() );
);
③y=f(x)的圖象關于(-![]() ,0)對稱;
,0)對稱;
④ y=f(x)的圖象關于直線x=-![]() 對稱;
對稱;
其中正確的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)若對任意的![]() 恒成立,求實數
恒成立,求實數![]() 的最小值.
的最小值.
(2)若![]() 且關于
且關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數![]() 的取值范圍;
的取值范圍;
(3)設各項為正的數列![]() 滿足:
滿足: ![]() 求證:
求證: ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com