
【題目】在直角坐標系中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)將曲線![]() 上各點的縱坐標伸長為原來的
上各點的縱坐標伸長為原來的![]() 倍(橫坐標不變)得到曲線
倍(橫坐標不變)得到曲線![]() ,求
,求![]() 的參數方程;
的參數方程;
(2)若![]() ,
,![]() 分別是直線
分別是直線![]() 與曲線
與曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 過點
過點![]() ,
,![]() 為其焦點,過
為其焦點,過![]() 且不垂直于
且不垂直于![]() 軸的直線
軸的直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,動點
兩點,動點![]() 滿足
滿足![]() 的垂心為原點
的垂心為原點![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)求證:動點![]() 在定直線
在定直線![]() 上,并求
上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知四邊形
中,已知四邊形![]() 是邊長為
是邊長為![]() 的正方形,點
的正方形,點![]() 在底面
在底面![]() 上的射影為底面
上的射影為底面![]() 的中心點
的中心點![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() 的面積為1.
的面積為1.
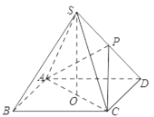
(1)若點![]() 是
是![]() 的中點,求證:平面
的中點,求證:平面![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在一點
上是否存在一點![]() 使得二面角
使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,說明理由.
的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業參加![]() 項目生產的工人為
項目生產的工人為![]() 人,平均每人每年創造利潤
人,平均每人每年創造利潤![]() 萬元.根據現實的需要,從
萬元.根據現實的需要,從![]() 項目中調出
項目中調出![]() 人參與
人參與![]() 項目的售后服務工作,每人每年可以創造利潤
項目的售后服務工作,每人每年可以創造利潤![]() 萬元(
萬元(![]() ),
),![]() 項目余下的工人每人每年創造利圖需要提高
項目余下的工人每人每年創造利圖需要提高![]()
(1)若要保證![]() 項目余下的工人創造的年總利潤不低于原來
項目余下的工人創造的年總利潤不低于原來![]() 名工人創造的年總利潤,則最多調出多少人參加
名工人創造的年總利潤,則最多調出多少人參加![]() 項目從事售后服務工作?
項目從事售后服務工作?
(2)在(1)的條件下,當從![]() 項目調出的人數不能超過總人數的
項目調出的人數不能超過總人數的![]() 時,才能使得
時,才能使得![]() 項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數
項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{2n﹣1}的前n項1,3,7,…,2n﹣1組成集合![]() (n∈N*),從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),記Sn=T1+T2+…+Tn,例如當n=1時,A1={1},T1=1,S1=1;當n=2時,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,試寫出Sn=__.
(n∈N*),從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),記Sn=T1+T2+…+Tn,例如當n=1時,A1={1},T1=1,S1=1;當n=2時,A2={1,3},T1=1+3,T2=1×3,S2=1+3+1×3=7,試寫出Sn=__.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 滿足
滿足![]() .
.
①存在![]() 可以生成的數列
可以生成的數列![]() 是常數數列;
是常數數列;
②“數列![]() 中存在某一項
中存在某一項![]() ”是“數列
”是“數列![]() 為有窮數列”的充要條件;
為有窮數列”的充要條件;
③若![]() 為單調遞增數列,則
為單調遞增數列,則![]() 的取值范圍是
的取值范圍是![]() ;
;
④只要![]() ,其中
,其中![]() ,則
,則![]() 一定存在;
一定存在;
其中正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》全稱《新編直指算法統宗》,是屮國古代數學名著,程大位著.書中有如下問題:“今有五人均銀四十兩,甲得十兩四錢,戊得五兩六錢.問:次第均之,乙丙丁各該若干?”意思是:有5人分40兩銀子,甲分10兩4錢,戊分5兩6錢,且相鄰兩項差相等,則乙丙丁各分幾兩幾錢?(注:1兩等于10錢)( )
A.乙分8兩,丙分8兩,丁分8兩B.乙分8兩2錢,丙分8兩,丁分7兩8錢
C.乙分9兩2錢,丙分8兩,丁分6兩8錢D.乙分9兩,丙分8兩,丁分7兩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個無窮數列![]() 分別滿足
分別滿足![]() ,
,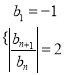 ,
,
其中![]() ,設數列
,設數列![]() 的前
的前![]() 項和分別為
項和分別為![]() ,
,
(1)若數列![]() 都為遞增數列,求數列
都為遞增數列,求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足:存在唯一的正整數
滿足:存在唯一的正整數![]() (
(![]() ),使得
),使得![]() ,稱數列
,稱數列![]() 為“
為“![]() 墜點數列”
墜點數列”
①若數列![]() 為“5墜點數列”,求
為“5墜點數列”,求![]() ;
;
②若數列![]() 為“
為“![]() 墜點數列”,數列
墜點數列”,數列![]() 為“
為“![]() 墜點數列”,是否存在正整數
墜點數列”,是否存在正整數![]() ,使得
,使得![]() ,若存在,求
,若存在,求![]() 的最大值;若不存在,說明理由.
的最大值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com