
【題目】某企業參加![]() 項目生產的工人為
項目生產的工人為![]() 人,平均每人每年創造利潤
人,平均每人每年創造利潤![]() 萬元.根據現實的需要,從
萬元.根據現實的需要,從![]() 項目中調出
項目中調出![]() 人參與
人參與![]() 項目的售后服務工作,每人每年可以創造利潤
項目的售后服務工作,每人每年可以創造利潤![]() 萬元(
萬元(![]() ),
),![]() 項目余下的工人每人每年創造利圖需要提高
項目余下的工人每人每年創造利圖需要提高![]()
(1)若要保證![]() 項目余下的工人創造的年總利潤不低于原來
項目余下的工人創造的年總利潤不低于原來![]() 名工人創造的年總利潤,則最多調出多少人參加
名工人創造的年總利潤,則最多調出多少人參加![]() 項目從事售后服務工作?
項目從事售后服務工作?
(2)在(1)的條件下,當從![]() 項目調出的人數不能超過總人數的
項目調出的人數不能超過總人數的![]() 時,才能使得
時,才能使得![]() 項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數
項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】某大型商場的空調在1月到5月的銷售量與月份相關,得到的統計數據如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
銷量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)經分析發現1月到5月的銷售量可用線性回歸模型擬合該商場空調的月銷量![]() (百件)與月份
(百件)與月份![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測6月份該商場空調的銷售量;
,并預測6月份該商場空調的銷售量;
(2)若該商場的營銷部對空調進行新一輪促銷,對7月到12月有購買空調意愿的顧客進行問卷調查.假設該地擬購買空調的消費群體十分龐大,經過營銷部調研機構對其中的500名顧客進行了一個抽樣調查,得到如下一份頻數表:
有購買意愿對應的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
頻數 | 60 | 80 | 120 | 130 | 80 | 30 |
現采用分層抽樣的方法從購買意愿的月份在7月與12月的這90名顧客中隨機抽取6名,再從這6人中隨機抽取3人進行跟蹤調查,求抽出的3人中恰好有2人是購買意愿的月份是12月的概率.
參考公式與數據:線性回歸方程![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 是遞增數列,數列
是遞增數列,數列![]() 滿足:對任意
滿足:對任意![]() ,存在
,存在![]() ,使得
,使得![]() ,則稱
,則稱![]() 是
是![]() 的“分隔數列”.
的“分隔數列”.
(1)設![]() ,證明:數列
,證明:數列![]() 是
是![]() 的分隔數列;
的分隔數列;
(2)設![]() 是
是![]() 的前n項和,
的前n項和,![]() ,判斷數列
,判斷數列![]() 是否是數列
是否是數列![]() 的分隔數列,并說明理由;
的分隔數列,并說明理由;
(3)設![]() 是
是![]() 的前n項和,若數列
的前n項和,若數列![]() 是
是![]() 的分隔數列,求實數
的分隔數列,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
:![]() ,左頂點為
,左頂點為![]() ,經過點
,經過點![]() ,過點
,過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,交
,交![]() 軸于點
軸于點![]() .
.
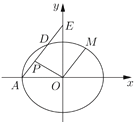
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為
為![]() 的中點,
的中點,![]() ,證明:對于任意的
,證明:對于任意的![]() 都有
都有![]() 恒成立;
恒成立;
(3)若過點![]() 作直線
作直線![]() 的平行線交橢圓
的平行線交橢圓![]() 于點
于點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩動圓![]() 和
和![]() (
(![]() ),把它們的公共點的軌跡記為曲線
),把它們的公共點的軌跡記為曲線![]() ,若曲線
,若曲線![]() 與
與![]() 軸的正半軸的交點為
軸的正半軸的交點為![]() ,且曲線
,且曲線![]() 上的相異兩點
上的相異兩點![]() 滿足:
滿足:![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)證明直線![]() 恒經過一定點,并求此定點的坐標;
恒經過一定點,并求此定點的坐標;
(3)求![]() 面積
面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 統計學中將
統計學中將![]() 個數
個數![]() 的和記作
的和記作![]()
(1)設![]()
![]() ,求
,求![]() ;
;
(2)是否存在互不相等的非負整數![]() ,
,![]() ,使得
,使得![]() 成立,若存在,請寫出推理的過程;若不存在請證明;
成立,若存在,請寫出推理的過程;若不存在請證明;
(3)設![]()
![]() 是不同的正實數,
是不同的正實數,![]() ,對任意的
,對任意的![]() ,都有
,都有![]() ,判斷
,判斷![]() 是否為一個等比數列,請說明理由.
是否為一個等比數列,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
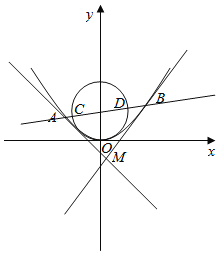
【題目】已知拋物線G的頂點在原點,焦點在y軸正半軸上,點P(m,4)到其準線的距離等于5.
(1)求拋物線G的方程;
(2)如圖,過拋物線G的焦點的直線依次與拋物線G及圓x2+(y﹣1)2=1交于A、C、D、B四點,試證明|AC||BD|為定值;
(3)過A、B分別作拋物G的切線l1,l2且l1,l2交于點M,試求△ACM與△BDM面積之和的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數據![]() ,
,![]() ,
,![]() ,
,![]() 是上海普通職
是上海普通職![]() (
(![]() ,
,![]() )個人的年收入,設這
)個人的年收入,設這![]() 個數據的中位數為
個數據的中位數為![]() ,平均數為
,平均數為![]() ,方差為
,方差為![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,則這
,則這![]() 個數據中,下列說法正確( )
個數據中,下列說法正確( )
A.年收入平均數大大增大,中位數一定變大,方差可能不變
B.年收入平均數大大增大,中位數可能不變,方差變大
C.年收入平均數大大增大,中位數可能不變,方差也不變
D.年收入平均數大大增大,中位數可能不變,方差可能不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 過點
過點![]() ,且漸近線方程為
,且漸近線方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于點
交于點![]() 、
、![]() 兩點.
兩點.
(1)求雙曲線![]() 的方程;
的方程;
(2)若直線![]() 過原點,點
過原點,點![]() 是曲線
是曲線![]() 上任一點,直線
上任一點,直線![]() ,
,![]() 的斜率都存在,記為
的斜率都存在,記為![]() 、
、![]() ,試探究
,試探究![]() 的值是否與點
的值是否與點![]() 及直線
及直線![]() 有關,并證明你的結論;
有關,并證明你的結論;
(3)若直線![]() 過點
過點![]() ,問在
,問在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為常數?若存在,求出點
為常數?若存在,求出點![]() 坐標及此常數的值;若不存在,說明理由.
坐標及此常數的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com