
【題目】已知兩動圓![]() 和
和![]() (
(![]() ),把它們的公共點的軌跡記為曲線
),把它們的公共點的軌跡記為曲線![]() ,若曲線
,若曲線![]() 與
與![]() 軸的正半軸的交點為
軸的正半軸的交點為![]() ,且曲線
,且曲線![]() 上的相異兩點
上的相異兩點![]() 滿足:
滿足:![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)證明直線![]() 恒經過一定點,并求此定點的坐標;
恒經過一定點,并求此定點的坐標;
(3)求![]() 面積
面積![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]() .
.
【解析】
(1)設兩動圓的公共點為![]() ,由橢圓定義得出曲線
,由橢圓定義得出曲線![]() 是橢圓,并得出
是橢圓,并得出![]() 、
、![]() 、
、![]() 的值,即可得出曲線
的值,即可得出曲線![]() 的方程;
的方程;
(2)求出點![]() ,設點
,設點![]() ,
,![]() ,對直線
,對直線![]() 的斜率是否存在分兩種情況討論,在斜率存在時,設直線
的斜率是否存在分兩種情況討論,在斜率存在時,設直線![]() 的方程為
的方程為![]() ,并將該直線方程與橢圓
,并將該直線方程與橢圓![]() 的方程聯立,列出韋達定理,結合條件
的方程聯立,列出韋達定理,結合條件![]() 并代入韋達定理求出
并代入韋達定理求出![]() 的值,可得出直線
的值,可得出直線![]() 所過點的坐標,在直線
所過點的坐標,在直線![]() 的斜率不存在時,可得出直線
的斜率不存在時,可得出直線![]() 的方程為
的方程為![]() ,結合這兩種情況得出直線
,結合這兩種情況得出直線![]() 所過定點坐標;
所過定點坐標;
(3)利用韋達定理求出![]() 面積
面積![]() 關于
關于![]() 的表達式,換元
的表達式,換元![]() ,然后利用基本不等式求出
,然后利用基本不等式求出![]() 的最大值.
的最大值.
(1)設兩動圓的公共點為![]() ,則有:
,則有:![]() .
.
由橢圓的定義可知![]() 的軌跡為橢圓,
的軌跡為橢圓,![]() ,
,![]() ,所以曲線
,所以曲線![]() 的方程是:
的方程是:![]() ;
;
(2)由題意可知:![]() ,設
,設![]() ,
,![]() ,
,
當![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() ,聯立方程組:
,聯立方程組:
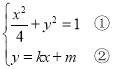 ,把②代入①有:
,把②代入①有:![]() ,
,
![]() ③,
③,![]() ④,
④,
因為![]() ,所以有
,所以有![]() ,
,
![]() ,把③④代入整理:
,把③④代入整理:
![]() ,(有公因式
,(有公因式![]() )繼續化簡得:
)繼續化簡得:
![]() ,
,![]() 或
或![]() (舍),
(舍),
當![]() 的斜率不存在時,易知滿足條件
的斜率不存在時,易知滿足條件![]() 的直線
的直線![]() 為:
為:![]()
過定點![]() ,綜上,直線
,綜上,直線![]() 恒過定點
恒過定點![]() ;
;
(3)![]() 面積
面積![]() ,
,
由第(2)小題的③④代入,整理得:![]() ,
,
因![]() 在橢圓內部,所以
在橢圓內部,所以![]() ,可設
,可設![]() ,
,
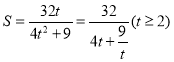 ,
,![]() ,
,![]() (
(![]() 時取到最大值).
時取到最大值).
所以![]() 面積
面積![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知點F1,F2分別為橢圓![]() 的左、右焦點,點P為橢圓上任意一點,P到焦點F2的距離的最大值為
的左、右焦點,點P為橢圓上任意一點,P到焦點F2的距離的最大值為![]() ,且△PF1F2的最大面積為1.
,且△PF1F2的最大面積為1.
(Ⅰ)求橢圓C的方程.
(Ⅱ)點M的坐標為![]() ,過點F2且斜率為k的直線L與橢圓C相交于A,B兩點.對于任意的
,過點F2且斜率為k的直線L與橢圓C相交于A,B兩點.對于任意的![]() 是否為定值?若是求出這個定值;若不是說明理由.
是否為定值?若是求出這個定值;若不是說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,
,![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() ,點
,點![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.

(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )若過點
)若過點![]() 且斜率不為
且斜率不為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,已知直線
兩點,已知直線![]() 與
與![]() 相交于點
相交于點![]() ,試判斷點
,試判斷點![]() 是否在定直線上?若是,請求出定直線的方程;若不是,請說明理由.
是否在定直線上?若是,請求出定直線的方程;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為正方體ABCD-A1B1C1D1,動點M從B1點出發,在正方體表面沿逆時針方向運動一周后,再回到B1的運動過程中,點M與平面A1DC1的距離保持不變,運動的路程x與l=MA1+MC1+MD之間滿足函數關系l=f(x),則此函數圖象大致是( )
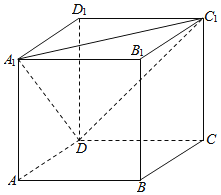
A. 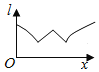 B.
B. 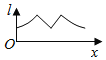
C. 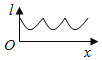 D.
D. 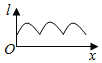
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業參加![]() 項目生產的工人為
項目生產的工人為![]() 人,平均每人每年創造利潤
人,平均每人每年創造利潤![]() 萬元.根據現實的需要,從
萬元.根據現實的需要,從![]() 項目中調出
項目中調出![]() 人參與
人參與![]() 項目的售后服務工作,每人每年可以創造利潤
項目的售后服務工作,每人每年可以創造利潤![]() 萬元(
萬元(![]() ),
),![]() 項目余下的工人每人每年創造利圖需要提高
項目余下的工人每人每年創造利圖需要提高![]()
(1)若要保證![]() 項目余下的工人創造的年總利潤不低于原來
項目余下的工人創造的年總利潤不低于原來![]() 名工人創造的年總利潤,則最多調出多少人參加
名工人創造的年總利潤,則最多調出多少人參加![]() 項目從事售后服務工作?
項目從事售后服務工作?
(2)在(1)的條件下,當從![]() 項目調出的人數不能超過總人數的
項目調出的人數不能超過總人數的![]() 時,才能使得
時,才能使得![]() 項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數
項目中留崗工人創造的年總利潤始終不低于調出的工人所創造的年總利潤,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的方程為
的方程為![]() ,其中常數
,其中常數![]() ,
,![]() 是拋物線
是拋物線![]() 的焦點.
的焦點.
(1)若直線![]() 被拋物線
被拋物線![]() 所截得的弦長為6,求
所截得的弦長為6,求![]() 的值;
的值;
(2)設![]() 是點
是點![]() 關于頂點
關于頂點![]() 的對稱點,
的對稱點,![]() 是拋物線
是拋物線![]() 上的動點,求
上的動點,求![]() 的最大值;
的最大值;
(3)設![]() ,
,![]() 、
、![]() 是兩條互相垂直,且均經過點
是兩條互相垂直,且均經過點![]() 的直線,
的直線,![]() 與拋物線
與拋物線![]() 交于點
交于點![]() 、
、![]() ,
,![]() 與拋物線
與拋物線![]() 交于點
交于點![]() 、
、![]() ,若點
,若點![]() 滿足
滿足![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前6項依次成等比數列,設公比為q(
的前6項依次成等比數列,設公比為q(![]() ),數列從第5項開始各項依次為等差數列,其中
),數列從第5項開始各項依次為等差數列,其中![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(1)求公比q及數列![]() 的通項公式;
的通項公式;
(2)若![]() ,求項數n的取值范圍.
,求項數n的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com