
分析 (1)由已知得:a1,a3,a8成等比數列,從而4d2=3a1d,由此能求出$\frac{a_1}p9vv5xb5$的值.
(2)設數列{kn}為等比數列,則${k_2}^2={k_1}{k_3}$,推導出$\frac{a_1}p9vv5xb5=1$,從而${a_{k_n}}={k_n}d$,進而${k_n}={k_1}{q^{n-1}}$.由此得到當$\frac{a_1}p9vv5xb5=1$時,數列{kn}為等比數列.
(3)由數列{kn}為等比數列,a1=d,${k_n}={k_1}{q^{n-1}}(q>1)$.得到${a_1}>\frac{{2{k_1}{q^{n-1}}}}{{n+{k_1}{q^{n-1}}}}$,$0<\frac{1}{a_1}<\frac{{n+{k_1}{q^{n-1}}}}{{2{k_1}{q^{n-1}}}}=\frac{1}{2}+\frac{q}{{2{k_1}}}\frac{n}{q^n}$恒成立,再證明對于任意的正實數ε(0<ε<1),總存在正整數n1,使得$\frac{n_1}{{{q^{n_1}}}}<ε$.
要證$\frac{n_1}{{{q^{n_1}}}}<ε$,即證lnn1<n1lnq+lnε.由此能求出a1的取值范圍.
解答 解:(1)由已知可得:a1,a3,a8成等比數列,
所以${({a_1}+2d)^2}={a_1}({a_1}+7d)$,…2分
整理可得:4d2=3a1d.
因為d≠0,所以$\frac{a_1}p9vv5xb5=\frac{4}{3}$. …4分
(2)設數列{kn}為等比數列,則${k_2}^2={k_1}{k_3}$.
又因為${a_{k_1}}$,${a_{k_2}}$,${a_{k_3}}$成等比數列,
所以$[{{a_1}+({k_1}-1)d}][{{a_1}+({k_3}-1)d}]={[{{a_1}+({k_2}-1)d}]^2}$.
整理,得${a_1}(2{k_2}-{k_1}-{k_3})=d({k_1}{k_3}-{k_2}^2-{k_1}-{k_3}+2{k_2})$.
因為${k_2}^2={k_1}{k_3}$,所以a1(2k2-k1-k3)=d(2k2-k1-k3).
因為2k2≠k1+k3,所以a1=d,即$\frac{a_1}p9vv5xb5=1$.…6分
當$\frac{a_1}p9vv5xb5=1$時,an=a1+(n-1)d=nd,所以${a_{k_n}}={k_n}d$.
又因為${a_{k_n}}={a_{k_1}}{q^{n-1}}={k_1}d{q^{n-1}}$,所以${k_n}={k_1}{q^{n-1}}$.
所以$\frac{{{k_{n+1}}}}{k_n}=\frac{{{k_1}{q^n}}}{{{k_1}{q^{n-1}}}}=q$,數列{kn}為等比數列.
綜上,當$\frac{a_1}p9vv5xb5=1$時,數列{kn}為等比數列.…8分
(3)因為數列{kn}為等比數列,由(2)知a1=d,${k_n}={k_1}{q^{n-1}}(q>1)$.
${a_{k_n}}={a_{k_1}}{q^{n-1}}={k_1}d{q^{n-1}}={k_1}{a_1}{q^{n-1}}$,an=a1+(n-1)d=na1.
因為對于任意n∈N*,不等式${a_n}+{a_{k_n}}>2{k_n}$恒成立.
所以不等式$n{a_1}+{k_1}{a_1}{q^{n-1}}>2{k_1}{q^{n-1}}$,
即${a_1}>\frac{{2{k_1}{q^{n-1}}}}{{n+{k_1}{q^{n-1}}}}$,$0<\frac{1}{a_1}<\frac{{n+{k_1}{q^{n-1}}}}{{2{k_1}{q^{n-1}}}}=\frac{1}{2}+\frac{q}{{2{k_1}}}\frac{n}{q^n}$恒成立.…10分
下面證明:對于任意的正實數ε(0<ε<1),總存在正整數n1,使得$\frac{n_1}{{{q^{n_1}}}}<ε$.
要證$\frac{n_1}{{{q^{n_1}}}}<ε$,即證lnn1<n1lnq+lnε.
因為$lnx≤\frac{1}{e}x<\frac{1}{2}x$,則$ln{n_1}=2ln{n_1}^{\frac{1}{2}}<{n_1}^{\frac{1}{2}}$,
解不等式${n_1}^{\frac{1}{2}}<{n_1}lnq+lnε$,即${({n_1}^{\frac{1}{2}})^2}lnq-{n_1}^{\frac{1}{2}}+lnε>0$,
可得${n_1}^{\frac{1}{2}}>\frac{{1+\sqrt{1-4lnqlnε}}}{2lnq}$,所以${n_1}>{(\frac{{1+\sqrt{1-4lnqlnε}}}{2lnq})^2}$.
不妨取${n_0}=[{{{(\frac{{1+\sqrt{1-4lnqlnε}}}{2lnq})}^2}}]+1$,則當n1>n0時,原式得證.
所以$0<\frac{1}{a_1}≤\frac{1}{2}$,所以a1≥2,即得a1的取值范圍是[2,+∞). …16分
點評 本題考查等差數列的首項與公差的比值的求法,考查滿足等比數列的等差數列的首項與公差的比值的確定,考查數列的首項的取值范圍的求法,綜合性強,難度大,對數學思維要求較高.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
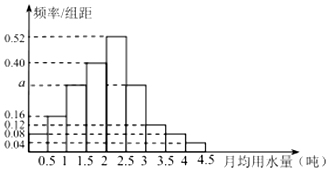 我國上是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準x(噸),用水量不超過x的部分按平價收費,超過x的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
我國上是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準x(噸),用水量不超過x的部分按平價收費,超過x的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com