
【題目】已知點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 為橢圓
為橢圓![]() 的右頂點,點
的右頂點,點![]() 是橢圓
是橢圓![]() 上不同的兩點(均異于
上不同的兩點(均異于![]() )且滿足直線
)且滿足直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .試判斷直線
.試判斷直線![]() 是否過定點,若是,求出定點坐標,若不是,說明理由.
是否過定點,若是,求出定點坐標,若不是,說明理由.
【答案】(1) ![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:(1)由點![]() 在橢圓
在橢圓![]() 上,且橢圓的離心率為
上,且橢圓的離心率為![]() ,結合性質
,結合性質![]() ,列出關于
,列出關于![]() 、
、![]() 、
、![]() 的方程組,求出
的方程組,求出![]() 、
、![]() 、
、![]() ,即可得橢圓
,即可得橢圓![]() 的方程;(2)由題意,直線
的方程;(2)由題意,直線![]() 的斜率存在,可設直線
的斜率存在,可設直線![]() 的方程為
的方程為![]() ,
, ![]() ,
, ![]() ,聯立
,聯立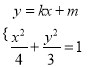 ,得
,得![]() ,根據韋達定理、斜率公式及直線
,根據韋達定理、斜率公式及直線![]() 與
與![]() 斜率之積為
斜率之積為![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() ,將以上結論代入直線方程即可得結果.
,將以上結論代入直線方程即可得結果.
試題解析:(1)可知離心率![]() ,故有
,故有![]() ,
,
![]()
又有點![]() 在橢圓
在橢圓![]() 上,代入得
上,代入得![]() ,
,
解得![]() ,
, ![]() ,
,
故橢圓![]() 的方程為
的方程為![]() .
.
(2)由題意,直線![]() 的斜率存在,可設直線
的斜率存在,可設直線![]() 的方程為
的方程為
![]() ,
, ![]() ,
, ![]() ,
,
聯立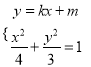 得
得![]() .
.
∴![]() ,
, ![]() .
.
∵直線![]() 與
與![]() 斜率之積為
斜率之積為![]() .
.
而點![]() ,∴
,∴![]() .
.
∴![]() .
.
化簡得![]() ,
,
∴![]() ,
,
化簡得![]() ,解得
,解得![]() 或
或![]() ,
,
當![]() 時,直線
時,直線![]() 的方程為直線
的方程為直線![]() 與
與![]() 斜率之積為
斜率之積為![]() ,過定點
,過定點![]() .
.
![]() 代入判別式大于零中,解得
代入判別式大于零中,解得![]() .
.
當![]() 時,直線
時,直線![]() 的方程為
的方程為![]() ,過定點
,過定點![]() ,不符合題意.
,不符合題意.
故直線![]() 過定點
過定點![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1: ![]() (t為參數,t≠0),其中0≤α<π.在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sin θ,C3:ρ=2
(t為參數,t≠0),其中0≤α<π.在以O為極點,x軸正半軸為極軸的極坐標系中,曲線C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2與C3交點的直角坐標;
(2)若C1與C2相交于點A,C1與C3相交于點B,求|AB|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,動點
為坐標原點,動點![]() 在橢圓
在橢圓![]() 上,過
上,過![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,點
,點![]() 滿足
滿足![]() .(Ⅰ)求點
.(Ⅰ)求點![]() 的軌跡方程
的軌跡方程![]() ;
;
(Ⅱ)過![]() 的直線
的直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點,過
兩點,過![]() 作與
作與![]() 垂直的直線
垂直的直線![]() 與點
與點![]() 的軌跡交于
的軌跡交于![]() 兩點,求證:
兩點,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
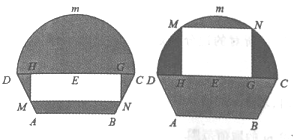
【題目】如圖所示的自動通風設施.該設施的下部![]() 是等腰梯形,其中
是等腰梯形,其中![]() 為2米,梯形的高為1米,
為2米,梯形的高為1米, ![]() 為3米,上部
為3米,上部![]() 是個半圓,固定點
是個半圓,固定點![]() 為
為![]() 的中點.
的中點. ![]() 是由電腦控制可以上下滑動的伸縮橫桿(橫桿面積可忽略不計),且滑動過程中始終保持和
是由電腦控制可以上下滑動的伸縮橫桿(橫桿面積可忽略不計),且滑動過程中始終保持和![]() 平行.當
平行.當![]() 位于
位于![]() 下方和上方時,通風窗的形狀均為矩形
下方和上方時,通風窗的形狀均為矩形![]() (陰影部分均不通風).
(陰影部分均不通風).
(1)設![]() 與
與![]() 之間的距離為
之間的距離為![]() (
(![]() 且
且![]() )米,試將通風窗的通風面積
)米,試將通風窗的通風面積![]() (平方米)表示成關于
(平方米)表示成關于![]() 的函數
的函數![]() ;
;
(2)當![]() 與
與![]() 之間的距離為多少米時,通風窗的通風面積
之間的距離為多少米時,通風窗的通風面積![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“累積凈化量(![]() )”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化器從開始使用到凈化效率為
)”是空氣凈化器質量的一個重要衡量指標,它是指空氣凈化器從開始使用到凈化效率為![]() 時對顆粒物的累積凈化量,以克表示.根據
時對顆粒物的累積凈化量,以克表示.根據![]() 《空氣凈化器》國家標準,對空氣凈化器的累計凈化量(
《空氣凈化器》國家標準,對空氣凈化器的累計凈化量(![]() )有如下等級劃分:
)有如下等級劃分:
累積凈化量(克) |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器(共2000臺)的質量,隨機抽取![]() 臺機器作為樣本進行估計,已知這
臺機器作為樣本進行估計,已知這![]() 臺機器的累積凈化量都分布在區間
臺機器的累積凈化量都分布在區間![]() 中.按照
中.按照![]() 均勻分組,其中累積凈化量在
均勻分組,其中累積凈化量在![]() 的所有數據有:
的所有數據有: ![]() 和
和![]() ,并繪制了如下頻率分布直方圖:
,并繪制了如下頻率分布直方圖:

(1)求![]() 的值及頻率分布直方圖中的
的值及頻率分布直方圖中的![]() 值;
值;
(2)以樣本估計總體,試估計這批空氣凈化器(共2000臺)中等級為![]() 的空氣凈化器有多少臺?
的空氣凈化器有多少臺?
(3)從累積凈化量在![]() 的樣本中隨機抽取2臺,求恰好有1臺等級為
的樣本中隨機抽取2臺,求恰好有1臺等級為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() , 若橢圓上一點
, 若橢圓上一點![]() 滿足
滿足![]() ,且橢圓
,且橢圓![]() 過點
過點![]() ,過點
,過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 是點
是點![]() 在
在![]() 軸上的垂足,延長
軸上的垂足,延長![]() 交橢圓
交橢圓![]() 于
于![]() ,求證:
,求證: ![]() 三點共線.
三點共線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com