【題目】已知橢圓
的左、右焦點分別為
且橢圓上存在一點
，滿足
.
(1)求橢圓
的標準方程；
(2)已知
分別是橢圓的左、右頂點，過
的直線交橢圓于
兩點，記直線
的交點為
，是否存在一條定直線
，使點恒在直線上?
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】“十三五”規劃確定了到2020年消除貧困的宏偉目標，打響了精準扶貧的攻堅戰，為完成脫貧任務，某單位在甲地成立了一家醫療器械公司吸納附近貧困村民就工，已知該公司生產某種型號醫療器械的月固定成本為20萬元，每生產1千件需另投入5.4萬元，設該公司一月內生產該型號醫療器械x千件且能全部銷售完，每千件的銷售收入為
萬元，已知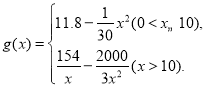
（1）請寫出月利潤y（萬元）關于月產量x（千件）的函數解析式；
（2）月產量為多少千件時，該公司在這一型號醫療器械的生產中所獲月利潤最大？并求出最大月利潤（精確到0.1萬元）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義：如果函數
的導函數為
，在區間
上存在
，
使得
，
，則稱為區間上的“雙中值函數“
已知函數
是
上的“雙中值函數“，則實數m的取值范圍是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知集合A={x|x2﹣x﹣2＞0}，函數g（x）=
的定義域為集合B，
（1）求A∩B和A∪B；
（2）若C={x|4x+p＜0}，且CA，求實數P的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市教學研究室為了對今后所出試題的難度有更好的把握，提高命題質量，對該市高三理科數學試卷的得分情況進行了調研．從全市參加考試的理科考生中隨機抽取了100名考生的數學成績（滿分150分），將數據分成9組：
，
，
，
，
，
，
，
，
，并整理得到如圖所示的頻率分布直方圖．用統計的方法得到樣本標準差
，以頻率值作為概率估計值．
（Ⅰ）根據頻率分布直方圖，求抽取的100名理科考生數學成績的平均分
及眾數
；
（Ⅱ）用頻率估計概率，從該市所有高三理科考生的數學成績中隨機抽取3個，記理科數學成績位于區間
內的個數為
，求的分布列及數學期望
；
（Ⅲ）從該市高三理科數學考試成績中任意抽取一份，記其成績為
，依據以下不等式評判（
表示對應事件的概率）：
①
，②
，
③
，其中
．
評判規則：若至少滿足以上兩個不等式，則給予這套試卷好評，否則差評．試問：這套試卷得到好評還是差評？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
，底面四邊形
為直角梯形，
，
，
為線段
上一點.
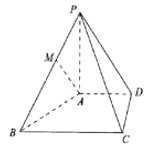
(1)若
，則在線段上是否存在點，使得
平面
?若存在，請確定點的位置；若不存在，請說明理由
(2)己知
，若異面直線
與
成
角，二而角
的余弦值為
，求的長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，直線
上有兩點E，F使
，點P在線段
的延長線上，且
.
（1）若
，求點P的軌跡方程；
（2）若在點P的軌跡上存在兩點M，N，設
，
的夾角為
.
①若
，求證：直線
過定點，并求定點坐標；
②若為銳角，求直線與x軸交點橫坐標的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為鼓勵應屆畢業大學生自主創業，國家對應屆畢業大學生創業貸款有貼息優惠政策，現有應屆畢業大學生甲貸款開小型超市，初期投入為72萬元，經營后每年的總收入為50萬元，該公司第
年需要付出的超市維護和工人工資等費用為
萬元，已知
為等差數列，相關信息如圖所示.
（Ⅰ）求；
（Ⅱ）該超市第幾年開始盈利？（即總收入減去成本及所有費用之差為正值）
（Ⅲ）該超市經營多少年，其年平均獲利最大？最大值是多少？（年平均獲利
）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
