
【題目】某市教學研究室為了對今后所出試題的難度有更好的把握,提高命題質量,對該市高三理科數學試卷的得分情況進行了調研.從全市參加考試的理科考生中隨機抽取了100名考生的數學成績(滿分150分),將數據分成9組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到如圖所示的頻率分布直方圖.用統計的方法得到樣本標準差
,并整理得到如圖所示的頻率分布直方圖.用統計的方法得到樣本標準差![]() ,以頻率值作為概率估計值.
,以頻率值作為概率估計值.

(Ⅰ)根據頻率分布直方圖,求抽取的100名理科考生數學成績的平均分![]() 及眾數
及眾數![]() ;
;
(Ⅱ)用頻率估計概率,從該市所有高三理科考生的數學成績中隨機抽取3個,記理科數學成績位于區間![]() 內的個數為
內的個數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() ;
;
(Ⅲ)從該市高三理科數學考試成績中任意抽取一份,記其成績為![]() ,依據以下不等式評判(
,依據以下不等式評判(![]() 表示對應事件的概率):
表示對應事件的概率):
①![]() ,②
,②![]() ,
,
③![]() ,其中
,其中![]() .
.
評判規則:若至少滿足以上兩個不等式,則給予這套試卷好評,否則差評.試問:這套試卷得到好評還是差評?
【答案】(Ⅰ)平均分![]() ,眾數
,眾數![]() ;(Ⅱ)分布列詳見解析,
;(Ⅱ)分布列詳見解析,![]() ;(Ⅲ)得到好評.
;(Ⅲ)得到好評.
【解析】
(Ⅰ)利用頻率分布直方圖估計平均數和眾數的方法可直接求得結果;
(Ⅱ)根據頻率分布直方圖計算可知理科數學成績位于![]() 內的概率為
內的概率為![]() ,則
,則![]() ,由此計算出
,由此計算出![]() 的每個取值對應的概率,由此得到分布列;由二項分布數學期望計算公式計算可得
的每個取值對應的概率,由此得到分布列;由二項分布數學期望計算公式計算可得![]() ;
;
(Ⅲ)計算每個區間取值所對應的概率與![]() 原則所對應的概率之間的大小關系,從而得到結論.
原則所對應的概率之間的大小關系,從而得到結論.
(Ⅰ)![]()
![]() ;
;
眾數:![]() ;
;
(Ⅱ)用頻率估計概率,可得從該市所有高三考生的理科數學成績中隨機抽取![]() 個,理科數學成績位于
個,理科數學成績位于![]() 內的概率為
內的概率為![]() ,則隨機變量
,則隨機變量![]() 服從二項分布
服從二項分布![]() ,故
,故![]() .
.
由題意知:![]() 所有可能的取值為
所有可能的取值為![]() ,
,
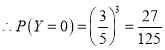 ;
;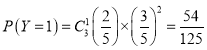 ;
;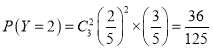 ;
;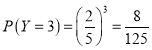 ;
;
![]() 的分布列為:
的分布列為:
|
|
|
|
|
|
|
|
|
|
數學期望![]() ;
;
(Ⅲ)記該市高三考生的理科數學成績為![]() ,由(Ⅰ)可知,
,由(Ⅰ)可知,![]() ,又
,又![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
符合②③,不符合①,![]() 這套試卷得到好評.
這套試卷得到好評.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】在5件產品中,有3件一等品和2件二等品,從中任取2件,以![]() 為概率的事件是( )
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】最近的一次數學競賽共6道試題,每題答對得7分,答錯(或不答)得0分.賽后某參賽代表隊獲團體總分161分,且統計分數時發現:該隊任兩名選手至多答對兩道相同的題目.沒有三名選手都答對兩道相同的題目.試問該隊選手至少有多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次投籃測試中,有兩種投籃方案:方案甲:先在A點投籃一次,以后都在B點投籃;方案乙:始終在B點投籃.每次投籃之間相互獨立.某選手在A點命中的概率為![]() ,命中一次記3分,沒有命中得0分;在B點命中的概率為
,命中一次記3分,沒有命中得0分;在B點命中的概率為![]() ,命中一次記2分,沒有命中得0分,用隨機變量
,命中一次記2分,沒有命中得0分,用隨機變量![]() 表示該選手一次投籃測試的累計得分,如果
表示該選手一次投籃測試的累計得分,如果![]() 的值不低于3分,則認為其通過測試并停止投籃,否則繼續投籃,但一次測試最多投籃3次.
的值不低于3分,則認為其通過測試并停止投籃,否則繼續投籃,但一次測試最多投籃3次.
(1)若該選手選擇方案甲,求測試結束后所得分![]() 的分布列和數學期望.
的分布列和數學期望.
(2)試問該選手選擇哪種方案通過測試的可能性較大?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓的2個焦點與1個短軸端點為頂點的三角形的面積為2
,以橢圓的2個焦點與1個短軸端點為頂點的三角形的面積為2![]() 。
。
(1)求橢圓的方程;
(2)如圖,斜率為k的直線l過橢圓的右焦點F,且與橢圓交與A,B兩點,以線段AB為直徑的圓截直線x=1所得的弦的長度為![]() ,求直線l的方程。
,求直線l的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如今我們的互聯網生活日益豐富,除了可以很方便地網購,網絡外賣也開始成為不少人日常生活中不可或缺的一部分.某市一調查機構針對該市市場占有率最高的甲、乙兩家網絡外賣企業(以下簡稱外賣甲,外賣乙)的經營情況進行了調查,調查結果如表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外賣甲日接單 | 5 | 2 | 9 | 8 | 11 |
外賣乙日接單 | 2.2 | 2.3 | 10 | 5 | 15 |
(1)據統計表明,![]() 與
與![]() 之間具有線性相關關系.
之間具有線性相關關系.
(ⅰ)請用相關系數![]() 加以說明:(若
加以說明:(若![]() ,則可認為
,則可認為![]() 與
與![]() 有較強的線性相關關系(
有較強的線性相關關系(![]() 值精確到0.001))
值精確到0.001))
(ⅱ)經計算求得![]() 與
與![]() 之間的回歸方程為
之間的回歸方程為![]() .假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于2500單時,外賣甲所獲取的日純利潤的大致范圍:(
.假定每單外賣業務企業平均能獲純利潤3元,試預測當外賣乙日接單量不低于2500單時,外賣甲所獲取的日純利潤的大致范圍:(![]() 值精確到0.01)
值精確到0.01)
(2)試根據表格中這五天的日接單量情況,從平均值和方差角度說明這兩家外賣企業的經營狀況.
相關公式:相關系數 ,
,
參考數據:![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,我國工業經濟發展迅速,工業增加值連年攀升,某研究機構統計了近十年(從2008年到2017年)的工業增加值(萬億元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工業增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依據表格數據,得到下面的散點圖及一些統計量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
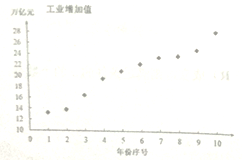
(1)根據散點圖和表中數據,此研究機構對工業增加值![]() (萬億元)與年份序號
(萬億元)與年份序號![]() 的回歸方程類型進行了擬合實驗,研究人員甲采用函數
的回歸方程類型進行了擬合實驗,研究人員甲采用函數![]() ,其擬合指數
,其擬合指數![]() ;研究人員乙采用函數
;研究人員乙采用函數![]() ,其擬合指數
,其擬合指數![]() ;研究人員丙采用線性函數
;研究人員丙采用線性函數![]() ,請計算其擬合指數,并用數據說明哪位研究人員的函數類型擬合效果最好.(注:相關系數
,請計算其擬合指數,并用數據說明哪位研究人員的函數類型擬合效果最好.(注:相關系數![]() 與擬合指數
與擬合指數![]() 滿足關系
滿足關系![]() ).
).
(2)根據(1)的判斷結果及統計值,建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);
的回歸方程(系數精確到0.01);
(3)預測到哪一年的工業增加值能突破30萬億元大關.
附:樣本![]()
![]() 的相關系數
的相關系數 ,
,
![]() ,
,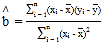 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com