
【題目】已知數列![]() 滿足
滿足![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() .
.
①求證:數列![]() 為等差數列;
為等差數列;
②求滿足![]() 的所有數對
的所有數對![]() .
.
【答案】(1)![]() ;(2)①見解析;②(10,4).
;(2)①見解析;②(10,4).
【解析】
(1)給![]() 中的n取值n=1,2,即得
中的n取值n=1,2,即得![]() 的值.(2) ①根據已知得到a2n=n+
的值.(2) ①根據已知得到a2n=n+![]() ,所以數列{a2n}為等差數列,公差為1.②先求出
,所以數列{a2n}為等差數列,公差為1.②先求出![]() ,再代入
,再代入![]() 得到(2m+p+9)(2m﹣p+3)=27,分析得到
得到(2m+p+9)(2m﹣p+3)=27,分析得到![]() ,從而得到滿足
,從而得到滿足![]() 的所有數對
的所有數對![]() .
.
(1)由![]() ,可得:
,可得: ,可得a1+a3=
,可得a1+a3=![]() .
.
(2)①∵![]() ,∴a2n﹣a2n﹣1=
,∴a2n﹣a2n﹣1=![]() ,a2n+1+a2n=
,a2n+1+a2n=![]() ,可得a2n+1+a2n﹣1=
,可得a2n+1+a2n﹣1=![]() .
.
∴1=![]() =(a1+a3)+(a3+a5)=4a3,解得a3=
=(a1+a3)+(a3+a5)=4a3,解得a3=![]() ,∴a1=
,∴a1=![]() .
.
∴a2n﹣1﹣![]() =﹣
=﹣![]() =……=(﹣1)n﹣1
=……=(﹣1)n﹣1![]() =0,解得a2n﹣1=
=0,解得a2n﹣1=![]() ,
,
可得a2n=n+![]() .
.
∴數列{a2n}為等差數列,公差為1.
②由①可得:a2n+1=a1,
∴S2n=a1+a2+……+a2n
=(a2+a3)+(a4+a5)+……+(a2n+a2n+1)
=![]() .
.
由滿足![]() ,可得:
,可得:![]() +3p=4
+3p=4![]() ,
,
化為:(2m+p+9)(2m﹣p+3)=27,
∵m,p∈N*,可得2m+p+9≥12,且2m+p+9,2m﹣p+3都為正整數,
∴![]() ,解得p=10,m=4.
,解得p=10,m=4.
故所求的數對為(10,4).


 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
【題目】在5件產品中,有3件一等品和2件二等品,從中任取2件,以![]() 為概率的事件是( )
為概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中數學 來源: 題型:
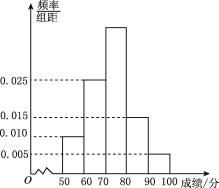
【題目】從2013年開始,國家教育部要求高中階段每學年都要組織學生進行學生體質健康測試,方案要求以學校為單位組織實施,某校對高一(1)班學生根據《國家學生體質健康標準》的測試項目按百分制進行了預備測試,并對50分以上的成績進行統計,其頻率分布直方圖如圖.所示,已知[90,100]分數段的人數為2.
(1)求[70,80)分數段的人數;
(2)現根據預備測試成績從成績在80分以上(含80分)的學生中任意選出2人代表班級參加學校舉行的一項體育比賽,求這2人的成績一個在[80,90)分數段、一個在[90,100]分數段的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(2)若函數![]() ,討論
,討論![]() 的單調性;
的單調性;
(3)若函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]() .設
.設![]() ,其中常數
,其中常數![]() 、
、![]() 滿足條件
滿足條件![]() ,且
,且![]() .試判斷在點
.試判斷在點![]() 處的切線斜率的正負,并說明理由.
處的切線斜率的正負,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定集合A={a1 , a2 , a3 , …,an}(n∈N* , n≥3)中,定義ai+aj(1≤i<j≤n,i,j∈N*)中所有不同值的個數為集合A兩元素和的容量,用L(A)表示.若數列{an}是公差不為0的等差數列,設集合A={a1 , a2 , a3 , …,a2016},則L(A)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)記F(x)=f(x)﹣g(x),判斷F(x)在區間(1,2)內零點個數并說明理由;
(Ⅱ)記(Ⅰ)中的F(x)在(1,2)內的零點為x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有兩個不等實根x1 , x2(x1<x2),判斷x1+x2與2x0的大小,并給出對應的證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直角坐標系xOy中,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ2﹣4ρsinθ+3=0,A、B兩點極坐標分別為(1,π)、(1,0).
(1)求曲線C的參數方程;
(2)在曲線C上取一點P,求|AP|2+|BP|2的最值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com