
【題目】如圖所示,已知點P在正方體ABCD-A′B′C′D′的對角線BD′上,∠PDA=60°.
(1)求DP與CC′所成角的大小.
(2)求DP與平面AA′D′D所成角的大小.
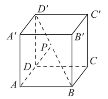
【答案】(1)45°.(2)30°.
【解析】
(1)以D為原點,DA,DC,DD′分別為x軸,y軸,z軸正方向建立空間直角坐標系,連接BD,B′D′.在平面BB′D′D中,延長DP交B′D′于H. 設![]() =(m,m,1)(m>0), 由<
=(m,m,1)(m>0), 由<![]() ,
,![]() >=60°,利用坐標運算可得m,進而可得cos<
>=60°,利用坐標運算可得m,進而可得cos<![]() ,
,![]() >,從而得解;
>,從而得解;
(2)平面AA′D′D的一個法向量是![]() =(0,1,0),由cos<
=(0,1,0),由cos<![]() ,
,![]() >即可得解.
>即可得解.
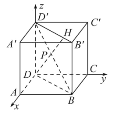
(1)如圖所示,以D為原點,DA,DC,DD′分別為x軸,y軸,z軸正方向建立空間直角坐標系,
設DA=1.則![]() =(1,0,0),
=(1,0,0),![]() =(0,0,1).連接BD,B′D′.在平面BB′D′D中,延長DP交B′D′于H.
=(0,0,1).連接BD,B′D′.在平面BB′D′D中,延長DP交B′D′于H.
設![]() =(m,m,1)(m>0),
=(m,m,1)(m>0),
由已知<![]() ,
,![]() >=60°,由
>=60°,由![]() ·
·![]() =|
=|![]() ||
||![]() |cos<
|cos<![]() ,
,![]() >,可得2m=
>,可得2m=![]() .解得m=
.解得m=![]() ,
,
所以![]() =
=![]() .
.
因為cos<![]() ,
,![]() >=
>=![]() =
=![]()
所以<![]() ,
,![]() >=45°,即DP與CC′所成的角為45°.
>=45°,即DP與CC′所成的角為45°.
(2)平面AA′D′D的一個法向量是![]() =(0,1,0),
=(0,1,0),
因為cos<![]() ,
,![]() >=
>=![]() =
=![]()
所以<![]() ,
,![]() >=60°,可得DP與平面AA′D′D所成的角為30°.
>=60°,可得DP與平面AA′D′D所成的角為30°.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】已知正項數列![]() 的前
的前![]() 項和為
項和為![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,它的前
,它的前![]() 項和為
項和為![]() ,
,
(ⅰ)求![]() ;
;
(ⅱ)若存在正整數![]() ,使不等式
,使不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不共線的向量![]() ,
,![]() 夾角為
夾角為![]() ,且
,且![]() ,
,![]() ,為正實數.
,為正實數.
(1)若![]() 與
與![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及對應的x的值,并指出此時向量
的最小值及對應的x的值,并指出此時向量![]() 與
與![]() 的位置關系.
的位置關系.
(3)若![]() 為銳角,對于正實數m,關于x的方程
為銳角,對于正實數m,關于x的方程![]() 兩個不同的正實數解,且
兩個不同的正實數解,且![]() ,求m的取值范圍.
,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
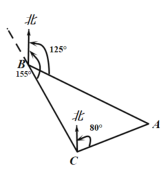
【題目】如圖,貨輪在海上B處,以50海里/時的速度沿方位角(從正北方向順時針轉到目標方向線的水平角)為155o的方向航行,為了確定船位,在B點處觀測到燈塔A的方位角為125o.半小時后,貨輪到達C點處,觀測到燈塔A的方位角為80o.求此時貨輪與燈塔之間的距離(答案保留最簡根號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列敘述錯誤的是( )
A.已知直線![]() 和平面
和平面![]() ,若點
,若點![]() ,點
,點![]() 且
且![]() ,
,![]() ,則
,則![]()
B.若三條直線兩兩相交,則三條直線確定一個平面
C.若直線![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,則
,則![]() 內的所有直線與
內的所有直線與![]() 都不相交
都不相交
D.若直線![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,則l至少與
,則l至少與![]() ,
,![]() 中的一條相交
中的一條相交
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率是40%.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定l,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果.經隨機模擬產生了如下10組隨機數:907 966 191 925 271 431 932 458 569 683.
據此估計,該運動員三次投籃恰有兩次命中的概率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com