
某種汽車購買時費用為14.4萬元,每年應交付保險費、養路費及汽油費共0.9萬元,汽車的維修費為:第一年0.2萬元,第二年0.4萬元,第三年0.6萬元,……,依等差數列逐年遞增.
(Ⅰ)設使用n年該車的總費用(包括購車費用)為f(n),試寫出f(n)的表達式;
(Ⅱ)求這種汽車使用多少年報廢最合算(即該車使用多少年平均費用最少)。
 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:解答題
已知數列{an}滿足:a1=1,a2=(a≠0),an+2=p·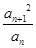 (其中P為非零常數,n∈N *)
(其中P為非零常數,n∈N *)
(1)判斷數列{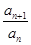 }是不是等比數列?
}是不是等比數列?
(2)求an;
(3)當a=1時,令bn=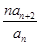 ,Sn為數列{bn}的前n項和,求Sn。
,Sn為數列{bn}的前n項和,求Sn。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)在平面直角坐標系中,已知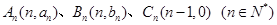 ,滿足向量
,滿足向量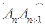 與向量
與向量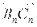 共線,且點
共線,且點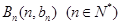 都在斜率為6的同一條直線上。若
都在斜率為6的同一條直線上。若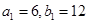 。求(1)數列
。求(1)數列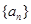 的通項
的通項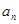 (2)數列{
(2)數列{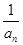 }的前n項和
}的前n項和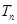
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分)
設數列{an}的前n項和為Sn=2n2,{bn}為等比數列,且a1=b1,b2(a2-a1)=b1.
(1)求數列{an}和{bn}的通項公式;
(2)設cn=,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知等比數列 的公比為q,記
的公比為q,記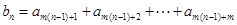 ,
,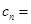
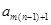 ·
·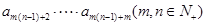 ,則以下結論一定正確的是( )
,則以下結論一定正確的是( )
A.數列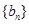 為等差數列,公差為 為等差數列,公差為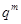 |
B.數列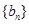 為等比數列,公比為 為等比數列,公比為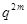 |
C.數列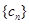 為等比數列,公比為 為等比數列,公比為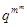 |
D.數列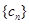 為等比數列,公比為 為等比數列,公比為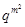 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知數列{an},{bn}滿足a1=b1=3,an+1-an=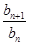 =3,n∈N*,若數列{cn}滿足cn=ban,則c2 013=( )
=3,n∈N*,若數列{cn}滿足cn=ban,則c2 013=( )
| A.92 012 | B.272 012 | C.92 013 | D.272 013 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com