【題目】(2015·浙江卷)已知數列{an}滿足a1＝
且an＋1＝an－
(n∈N*).
(1)證明：1≤
≤2(n∈N*)；
(2)設數列{
}的前n項和為Sn，證明： 
(n∈N*).
【答案】(1)見解析(2)見解析
【解析】試題分析：（Ⅰ）根據已知條件確定數列{an}為遞減數列，得到
，再由數列遞推可得到
，從而得到
的取值范圍。
（Ⅱ）根據已知條件確定
關于
的表達式，再由（Ⅰ）中的結論得到
的取值范圍，即可確定
的范圍。
試題解析： (1)由題意得an＋1－an＝－a
≤0，即an＋1≤an，
故an≤
.由an＝(1－an－1)an－1得
an＝(1－an－1)(1－an－2)…(1－a1)a1>0.
由0<an≤得
＝
＝
∈(1，2]，
即1≤≤2成立.
(2)由題意得
a＝an－an＋1，所以Sn＝a1－an＋1.①
由
－
＝和1≤≤2得1≤－≤2，
所以n≤－
≤2n，
因此
≤an＋1≤
(n∈N*).②
由①②得
≤
≤ (n∈N*).
名師導航單元期末沖刺100分系列答案
名校名卷單元同步訓練測試題系列答案科目：高中數學 來源： 題型：
【題目】已知函數
恰有3個零點，則實數
的取值范圍為（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
,在
上單調遞減.若
,則
在
上遞增,那么零點個數至多有一個,不符合題意,故
.故需
當
時
,且
,使得第一段有一個零點,故
.對于第二段, 
,故需
在區間
有兩個零點, 
,故
在
上遞增,在
上遞減,所以
,解得
.綜上所述, 
【點睛】本小題主要考查函數的圖象與性質,考查含有參數的分段函數零點問題的求解策略,考查了利用導數研究函數的單調區間,極值,最值等基本問題.其中用到了多種方法,首先對于第一段函數的分析利用了分離常數法,且直接看出函數的單調性.第二段函數利用的是導數來研究圖像與性質.
【題型】單選題
【結束】
13
【題目】設
， 
滿足約束條件
，則
的最大值為_______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】小王在某社交網 絡的朋友圈中，向在線的甲、乙、丙隨機發放紅包，每次發放1個．
(1)若小王發放5元的紅包2個，求甲恰得1個的概率；
(2)若小王發放3個紅包，其中5元的2個，10元的1個,記乙所得紅包的總錢數為X，求X的分布列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖
所示，一條直角走廊寬為
，
（1）若位于水平地面上的一根鐵棒在此直角走廊內，且
，試求鐵棒的長
；
（2）若一根鐵棒能水平地通過此直角走廊，求此鐵棒的最大長度；
（3）現有一輛轉動靈活的平板車，其平板面是矩形，它的寬
為
如圖2.平板車若想順利通過直角走廊，其長度不能超過多少米？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝ln(x＋1)＋
(a∈R)．
(1)當a＝1時，求函數f(x)在點(0，f(0))處的切線方程；
(2)討論函數f(x)的極值；
(3)求證：ln(n＋1)> 
(n∈N*)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}是等差數列，a1=f（x+1），a2=0，a3=f（x-1），其中f（x）=x2-4x+2．
（1）求通項公式an；
（2）若數列{an}為遞增數列，令bn=an+1+an+2+an+3+an+4，求數列{
}的前n項和Sn．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四棱錐
的底面
為直角梯形，
，
，
，
為正三角形.
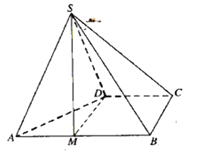
（1）點
為棱
上一點，若
平面
，
，求實數
的值；
（2）求點B到平面SAD的距離.
【答案】（1）
；（2）
【解析】試題分析：（1）由平面，可證
，進而證得四邊形
為平行四邊形，根據，可得
；
（2）利用等體積法
可求點
到平面
的距離.
試題解析：（（1）因為
平面SDM，
平面ABCD，
平面SDM 
平面ABCD=DM，
所以
，
因為
，所以四邊形BCDM為平行四邊形，又
，所以M為AB的中點.
因為
，
.
（2）因為
， 
，
所以平面
，
又因為
平面，
所以平面
平面，
平面
平面
，
在平面內過點
作
直線于點
，則平面，
在
和
中，
因為
，所以
，
又由題知
，
所以
，
由已知求得
，所以
，
連接BD，則
，
又求得
的面積為
，
所以由點B 到平面的距離為
.
【題型】解答題
【結束】
19
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作，該公司給出了兩種日薪薪酬方案.甲方案：底薪100元，每派送一單獎勵1元；乙方案：底薪140元，每日前55單沒有獎勵，超過55單的部分每單獎勵12元.
（1）請分別求出甲、乙兩種薪酬方案中日薪
（單位：元）與送貨單數
的函數關系式；
（2）根據該公司所有派送員100天的派送記錄，發現派送員的日平均派送單數與天數滿足以下表格：
日均派送單數 | 52 | 54 | 56 | 58 | 60 |
頻數（天） | 20 | 30 | 20 | 20 | 10 |
回答下列問題：
①根據以上數據，設每名派送員的日薪為
（單位：元），試分別求出這100天中甲、乙兩種方案的日薪
平均數及方差；
②結合①中的數據，根據統計學的思想，幫助小明分析，他選擇哪種薪酬方案比較合適，并說明你的理由.
（參考數據： 
， 
， 
， 
， 
， 
， 
， 
， 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等比數列
的公比
，前
項和為
，且滿足
.
，
，
分別是一個等差數列的第1項，第2項，第5項.
（1）求數列的通項公式；
（2）設
，求數列
的前項和
；
（3）若
，
的前項和為
，且對任意的
滿足
，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
