
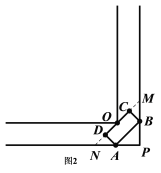
【題目】如圖![]() 所示,一條直角走廊寬為
所示,一條直角走廊寬為![]() ,
,![]()


(1)若位于水平地面上的一根鐵棒在此直角走廊內,且![]() ,試求鐵棒的長
,試求鐵棒的長![]() ;
;
(2)若一根鐵棒能水平地通過此直角走廊,求此鐵棒的最大長度;
(3)現有一輛轉動靈活的平板車,其平板面是矩形,它的寬![]() 為
為![]()
![]() 如圖2.平板車若想順利通過直角走廊,其長度
如圖2.平板車若想順利通過直角走廊,其長度![]() 不能超過多少米?
不能超過多少米?
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]()
![]()
(3)![]()
![]()
【解析】
(1)在圖1中,過點![]() 作
作![]() ,
,![]() 的垂線,垂直分別為
的垂線,垂直分別為![]() ,
,![]() ,則
,則![]() ,
,![]() ,在
,在![]() ,
,![]() 中,分別求解
中,分別求解![]() ,
,![]() 再相加,即可.
再相加,即可.
(2)由(1)可知,![]() ,令
,令![]() ,
,![]() 則
則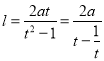 ,判斷單調性,再求最小值,即可.
,判斷單調性,再求最小值,即可.
(3)延長![]() 分別交
分別交![]() ,
,![]() 于
于![]() ,
,![]() ,設
,設![]() ,則
,則![]() .由(1)可知
.由(1)可知![]() ,在
,在![]() ,
,![]() 中分別計算
中分別計算![]() ,
,![]() ,則
,則![]() ,即
,即![]() ,令
,令![]() ,
,![]() 則
則![]() ,判斷單調性,再求最小值,即可
,判斷單調性,再求最小值,即可
(1)在圖1中,過點![]() 作
作![]() ,
,![]() 的垂線,垂直分別為
的垂線,垂直分別為![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
在![]() 中
中![]()
在![]() 中
中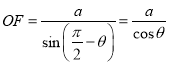
則![]()
即![]() ,
,![]() ,
,![]() ,
,![]() .
.

(2)由(1)可知![]() ,
,![]() .
.
令![]() ,則
,則![]()
即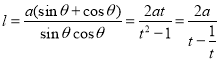
當![]() 時,
時,![]() 單調遞增,
單調遞增,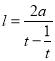 單調遞減.
單調遞減.
則![]() 即
即![]() 時
時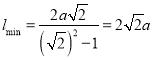
若一根鐵棒能水平地通過此直角走廊,則需此鐵棒的最大長度為![]()
![]()
(3)延長![]() 分別交
分別交![]() ,
,![]() 于
于![]() ,
,![]() ,設
,設![]() ,則
,則![]() .
.
由(1)可知![]() ,
,
在![]() 中,
中,![]()
在![]() 中,
中,![]()
則![]()
![]()
![]()
令![]() ,
,![]() 則
則![]()
即![]() ,
,![]() ,
,![]() .
.
當![]() 時
時![]() 單調遞減.
單調遞減.
則![]() 即
即![]() 時
時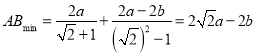 .
.
平板車若想順利通過直角走廊,其長度![]() 不能超過
不能超過![]()
![]()


科目:高中數學 來源: 題型:
【題目】設函數f(x)=ax2-a-lnx,其中a ∈R.
(I)討論f(x)的單調性;
(II)確定a的所有可能取值,使得![]() 在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
在區間(1,+∞)內恒成立(e=2.718…為自然對數的底數)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠家具車間造![]() 、
、![]() 型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張
型兩類桌子,每張桌子需木工和漆工梁道工序完成.已知木工做一張![]() 、
、![]() 型型桌子分別需要1小時和2小時,漆工油漆一張
型型桌子分別需要1小時和2小時,漆工油漆一張![]() 、
、![]() 型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張
型型桌子分別需要3小時和1小時;又知木工、漆工每天工作分別不得超過8小時和9小時,而工廠造一張![]() 、
、![]() 型型桌子分別獲利潤2千元和3千元.
型型桌子分別獲利潤2千元和3千元.
(1)列出滿足生產條件的數學關系式,并畫出可行域;
(2)怎樣分配生產任務才能使每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,現從參與調查的人群中隨機選出20人的樣本,并將這20人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示
,得到的頻率分布直方圖如圖所示

(1)求a的值.
(2)根據頻率分布直方圖,估計參與調查人群的樣本數據的![]() 分位數(保留兩位小數).
分位數(保留兩位小數).
(3)若從年齡在![]() 的人中隨機抽取兩位,求兩人恰有一人的年齡在
的人中隨機抽取兩位,求兩人恰有一人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學高考結束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學生進行問卷調查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數據b,c;
(2)判斷是否有99%的把握認為觀看2018年足球世界杯比賽與性別有關;
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發現它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現有問題:在打算觀看2018年足球世界杯比賽的同學中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·紹興仿真考試)已知數列{an}的奇數項依次構成公差為d1的等差數列,偶數項依次構成公差為d2的等差數列(其中d1,d2為整數),且對任意n∈N*,都有an<an+1,若a1=1,a2=2,且數列{an}的前10項和S10=75,則d1=________,a8=________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·浙江卷)已知數列{an}滿足a1=![]() 且an+1=an-
且an+1=an-![]() (n∈N*).
(n∈N*).
(1)證明:1≤![]() ≤2(n∈N*);
≤2(n∈N*);
(2)設數列{![]() }的前n項和為Sn,證明:
}的前n項和為Sn,證明: ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高三年級學生參加社區服務次數進行統計,隨機抽取M名學生作為樣本,得到這M名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表如下,頻率分布直方圖如圖:
分組 | 頻數 | 頻率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合計 | M | 1 |

(1)求出表中M,p及圖中a的值;
(2)若該校高三學生有240人,試估計該校高三學生參加社區服務的次數在區間[10,15)內的人數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至多一人參加社區服務次數在區間[25,30)內的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com