
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點 在橢圓上.
在橢圓上.
(![]() )求橢圓
)求橢圓![]() 的方程.
的方程.
(![]() )設動直線
)設動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,判斷是否存在以原點
有且僅有一個公共點,判斷是否存在以原點![]() 為圓心的圓,滿足此圓與
為圓心的圓,滿足此圓與![]() 相交于兩點
相交于兩點![]() ,
, ![]() (兩點均不在坐標軸上),且使得直線
(兩點均不在坐標軸上),且使得直線![]() 、
、![]() 的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
【答案】(1) 橢圓方程為![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(I)借助題設條件建立方程組求解;(II)借助題設運用直線與橢圓的位置關系推證和探求.
試題解析:
(I)由題意得: ![]() ,
, ![]() ,
,
又點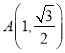 在橢圓
在橢圓![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
∴橢圓![]() 的方程為
的方程為![]() .………………5分
.………………5分
(II)存在符合條件的圓,且此圓的方程為![]() .
.
證明如下:假設存在符合條件的圓,并設此圓的方程為![]() .
.
當直線![]() 的斜率存在時,設
的斜率存在時,設![]() 的方程為
的方程為![]() .
.
由方程組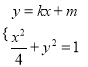 得
得![]() .
.
∵直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,
有且僅有一個公共點,
∴![]() ,即
,即![]() .
.
由方程組![]() 得
得![]() ,
,
則![]() .
.
設![]() ,則
,則![]() ,
,![]() ,
,
設直線![]() 的斜率分別為
的斜率分別為![]() ,
,
∴![]()
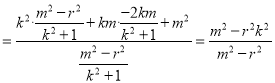 ,將
,將![]() 代入上式,
代入上式,
得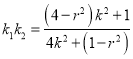 .
.
要使得![]() 為定值,則
為定值,則![]() ,即
,即![]() ,代入
,代入![]() 驗證知符合題意.
驗證知符合題意.
∴當圓的方程為![]() 時,圓與
時,圓與![]() 的交點
的交點![]() 滿足
滿足![]() 為定值
為定值![]() .
.
當直線![]() 的斜率不存在時,由題意知
的斜率不存在時,由題意知![]() 的方程為
的方程為![]() .
.
此時,圓![]() 與
與![]() 的交點
的交點![]() 也滿足
也滿足![]() .
.
綜上,當圓的方程為![]() 時,
時,
圓與![]() 的交點
的交點![]() 滿足直線
滿足直線![]() 的斜率之積為定值
的斜率之積為定值![]() .……………………12分
.……………………12分


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
【題目】設點![]() 是棱長為2的正方體
是棱長為2的正方體![]() 的棱
的棱![]() 的中點,點
的中點,點![]() 在面
在面![]() 所在的平面內,若平面
所在的平面內,若平面![]() 分別與平面
分別與平面![]() 和平面
和平面![]() 所成的銳二面角相等,則點
所成的銳二面角相等,則點![]() 到點
到點![]() 的最短距離是( )
的最短距離是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區為了提高小區內人員的讀書興趣,特舉辦讀書活動,準備進一定量的書籍豐富小區圖書站,由于不同年齡段需要看不同類型的書籍,為了合理配備資源,現對小區看書人員進行年齡調查,隨機抽取了一天40名讀書者進行調查,將他們的年齡分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖所示的頻率分布直方圖,問:
后得到如圖所示的頻率分布直方圖,問:
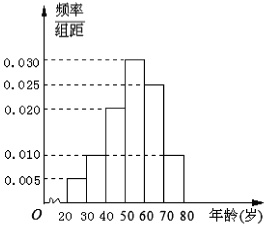
(1)在40名讀書者中年齡分布在![]() 的人數;
的人數;
(2)估計40名讀書者年齡的平均數和中位數;
(3)若從年齡在![]() 的讀書者中任取2名,求這兩名讀書者年齡在
的讀書者中任取2名,求這兩名讀書者年齡在![]() 的人數
的人數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在吸煙與患肺癌這兩個分類變量的獨立性檢驗的計算中,下列說法正確的是( )
A. 若![]() 的觀測值為
的觀測值為![]() ,在犯錯誤的概率不超過
,在犯錯誤的概率不超過![]() 的前提下認為吸煙與患肺癌有關系,那么在100個吸煙的人中必有99人患有肺癌.
的前提下認為吸煙與患肺癌有關系,那么在100個吸煙的人中必有99人患有肺癌.
B. 由獨立性檢驗可知,在犯錯誤的概率不超過![]() 的前提下認為吸煙與患肺癌有關系時,我們說某人吸煙,那么他有
的前提下認為吸煙與患肺癌有關系時,我們說某人吸煙,那么他有![]() 的可能患有肺癌.
的可能患有肺癌.
C. 若從統計量中求出在犯錯誤的概率不超過![]() 的前提下認為吸煙與患肺癌有關系,是指有
的前提下認為吸煙與患肺癌有關系,是指有![]() 的可能性使得判斷出現錯誤.
的可能性使得判斷出現錯誤.
D. 以上三種說法都不正確.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com