【題目】已如橢圓
，四點
中恰有三點在橢圓上.
（1）求橢圓C的方程；
（2）設不經過左焦點的直線
交橢圓于A，B兩點，若直線
、、
的斜率依次成等差數列，求直線l的斜率k的取值范圍.
【答案】（1）
（2）
或
.
【解析】
(1)先判斷
在橢圓上，然后再代入坐標進行判斷，即可求解出橢圓的方程；
(2)聯立直線與橢圓方程，根據斜率成等差數列求解出直線方程中
之間的關系，再根據聯立后的一元二次方程的
即可求解出斜率
的取值范圍.
解：（1）由橢圓的對稱性，點
在橢圓上，代入橢圓可得，
,
若點
在橢圓上，
則有
，聯立無解，
所以點
在橢圓上，代入橢圓可得，
，
代入中解得，
，
所以橢圓C的方程的為.
（2）由（1）可知
，
設直線AB的方程為，
，
聯立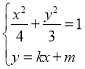
，
消y可得，
，
則有
，
①，
由題意可知，
，
化簡整理可得，
，
若
，則直線AB的方程為
，過點，不滿足題意
所以
，即
，
化簡可得，
，
代入①中得，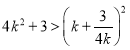
，
整理可得
，
解得
，
所以直線l的斜率k的取值范圍為或.
沖刺100分單元優化練考卷系列答案科目：高中數學 來源： 題型：
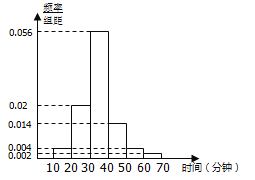
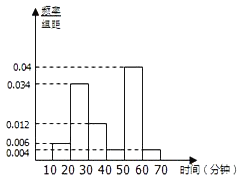
【題目】隨著移動互聯網的發展，與餐飲美食相關的手機APP軟件層出不窮.現從某市使用A和B兩款訂餐軟件的商家中分別隨機抽取100個商家，對它們的“平均送達時間”進行統計，得到頻率分布直方圖如下.
（1）已知抽取的100個使用A款訂餐軟件的商家中，甲商家的“平均送達時間”為18分鐘。現從使用A款訂餐軟件的商家中“平均送達時間”不超過20分鐘的商家中隨機抽取3個商家進行市場調研，求甲商家被抽到的概率；
（2）試估計該市使用A款訂餐軟件的商家的“平均送達時間”的眾數及平均數；
（3）如果以“平均送達時間”的平均數作為決策依據，從A和B兩款訂餐軟件中選擇一款訂餐，你會選擇哪款？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4－4：坐標系與參數方程]
在平面直角坐標系
中,以
為極點，
軸的正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
；直線
的參數方程為
(t為參數）.直線與曲線分別交于
兩點.
（1）寫出曲線的直角坐標方程和直線的普通方程；
（2）若點
的極坐標為
，
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從盛滿2升純酒精的容器里倒出1升純酒精,然后填滿水,再倒出1升混合溶液后又用水填滿,以此繼續下去,則至少應倒 次后才能使純酒精體積與總溶液的體積之比低于10%.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中，圓
：
經過伸縮變換
，后得到曲線
以坐標原點為極點，x軸的正半軸為極軸，并在兩種坐標系中取相同的單位長度，建立極坐標系，直線l的極坐標方程為
求曲線的直角坐標方程及直線l的直角坐標方程；
在上求一點M，使點M到直線l的距離最小，并求出最小距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的左、右焦點分別為
、
，過的直線
與橢圓相交于
、
兩點．
（1）求
的周長；
（2）設點
為橢圓的上頂點，點在第一象限，點
在線段
上．若
，求點的橫坐標；
（3）設直線不平行于坐標軸，點
為點關于
軸的對稱點，直線
與軸交于點
．求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，
，
，
，
的面積為
．
（1）求橢圓
的方程；
（2）過右焦點
作與
軸不重合的直線
交橢圓于
，
兩點，連接
，
分別交直線
于，
，
兩點，若直線
，
的斜率分別為
，
，試問：
是否為定值？若是，求出該定值，若不是，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
