
【題目】已知函數(shù)![]() .
.
(Ⅰ)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當(dāng)![]() ,
,![]() 時,
時,![]() ,其中
,其中![]() ,證明:
,證明:![]() .
.
【答案】(Ⅰ)見解析(Ⅱ)見解析
【解析】
(Ⅰ)依題意![]() ,再對
,再對![]() 分類討論求出函數(shù)
分類討論求出函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)由題得![]() ,分析得到只需證
,分析得到只需證![]() 時,
時,![]() 成立即可. 令
成立即可. 令![]() ,證明
,證明![]() 即得證.
即得證.
(Ⅰ)依題意,![]() ,
,![]() .
.
當(dāng)![]() 時,
時,![]() .
.
所以當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() .
.
所以函數(shù)![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
當(dāng)![]() 時,令
時,令![]() ,解得
,解得![]() 或
或![]() .
.
若![]() ,則
,則![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
若![]() ,則
,則![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減;
上單調(diào)遞減;
若![]() ,則
,則![]() ,
,
所以當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,所以函數(shù)
,所以函數(shù)![]() 在
在![]() 和
和![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(Ⅱ)依題意,得![]() ,所以
,所以![]() .
.
要證![]() ,即證
,即證![]() ,即證
,即證![]() ,即證
,即證![]() ,
,
即證![]() ,所以只需證
,所以只需證![]() 時,
時,![]() 成立即可.
成立即可.
令![]() ,則
,則![]() .
.
令![]() ,則
,則![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上單調(diào)遞增.所以
上單調(diào)遞增.所以![]() ,
,
所以![]() ,即
,即![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題![]() :關(guān)于
:關(guān)于![]() 的不等式
的不等式![]() 無解;命題
無解;命題![]() :指數(shù)函數(shù)
:指數(shù)函數(shù)![]() 是
是![]() 上的增函數(shù).
上的增函數(shù).
(1)若命題![]() 為真命題,求實數(shù)
為真命題,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若滿足![]() 為假命題且
為假命題且![]() 為真命題的實數(shù)
為真命題的實數(shù)![]() 取值范圍是集合
取值范圍是集合![]() ,集合
,集合![]() ,且
,且![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
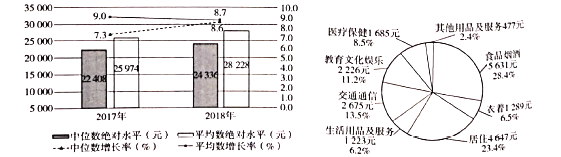
【題目】條形圖給出的是2017年全年及2018年全年全國居民人均可支配收入的平均數(shù)與中位數(shù),餅圖給出的是2018年全年全國居民人均消費及其構(gòu)成,現(xiàn)有如下說法:
①2018年全年全國居民人均可支配收入的平均數(shù)的增長率低于2017年;
②2018年全年全國居民人均可支配收入的中位數(shù)約是平均數(shù)的![]() ;
;
③2018年全年全國居民衣(衣著)食(食品煙酒)住(居住)行(交通通信)的支出超過人均消費的![]() .
.
則上述說法中,正確的個數(shù)是( )
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
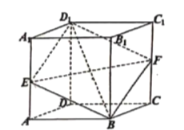
【題目】如圖所示,直平行六面體![]() 的所有棱長都為2,
的所有棱長都為2,![]() ,過體對角線
,過體對角線![]() 的截面S與棱
的截面S與棱![]() 和
和![]() 分別交于點E、F,給出下列命題中:
分別交于點E、F,給出下列命題中:
①四邊形![]() 的面積最小值為
的面積最小值為![]() ;
;
②直線EF與平面![]() 所成角的最大值為
所成角的最大值為![]() ;
;
③四棱錐![]() 的體積為定值;
的體積為定值;
④點![]() 到截面S的距離的最小值為
到截面S的距離的最小值為![]() .
.
其中,所有真命題的序號為( )
A.①②③B.①③④C.①③D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,
兩點,![]() 不與
不與![]() 軸垂直,圓
軸垂直,圓![]() .
.
(1)若點![]() 在橢圓
在橢圓![]() 上,點
上,點![]() 在圓
在圓![]() 上,求
上,求![]() 的最大值;
的最大值;
(2)若過線段![]() 的中點
的中點![]() 且垂直于
且垂直于![]() 的直線
的直線![]() 過點
過點![]() ,求直線
,求直線![]() 的斜率的取值范圍.
的斜率的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
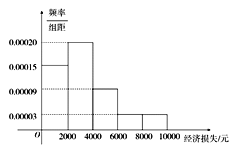
【題目】2014年7月18日15時,超強臺風(fēng)“威馬遜”登陸海南省.據(jù)統(tǒng)計,本次臺風(fēng)造成全省直接經(jīng)濟(jì)損失119.52億元.適逢暑假,小明調(diào)查住在自己小區(qū)的50戶居民由于臺風(fēng)造成的經(jīng)濟(jì)損失,作出如下頻率分布直方圖:
經(jīng)濟(jì)損失 4000元以下 | 經(jīng)濟(jì)損失 4000元以上 | 合計 | |
捐款超過500元 | 30 | ||
捐款低于500元 | 6 | ||
合計 |
(1)臺風(fēng)后區(qū)委會號召小區(qū)居民為臺風(fēng)重災(zāi)區(qū)捐款,小明調(diào)查的50戶居民捐款情況如上表,在表格空白處填寫正確數(shù)字,并說明是否有![]() 以上的把握認(rèn)為捐款數(shù)額是否多于或少于500元和自身經(jīng)濟(jì)損失是否到4000元有關(guān)?
以上的把握認(rèn)為捐款數(shù)額是否多于或少于500元和自身經(jīng)濟(jì)損失是否到4000元有關(guān)?
(2)臺風(fēng)造成了小區(qū)多戶居民門窗損壞,若小區(qū)所有居民的門窗均由李師傅和張師傅兩人進(jìn)行維修,李師傅每天早上在7:00到8:00之間的任意時刻來到小區(qū),張師傅每天早上在7:30到8:30分之間的任意時刻來到小區(qū),求連續(xù)3天內(nèi),李師傅比張師傅早到小區(qū)的天數(shù)的數(shù)學(xué)期望.
附:臨界值表
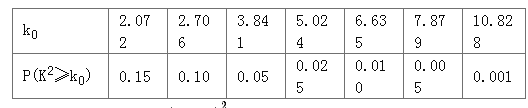
參考公式: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已如橢圓![]()
![]() ,四點
,四點![]()
![]()
![]()
![]() 中恰有三點在橢圓上.
中恰有三點在橢圓上.
(1)求橢圓C的方程;
(2)設(shè)不經(jīng)過左焦點的直線![]() 交橢圓于A,B兩點,若直線
交橢圓于A,B兩點,若直線![]() 、
、![]() 、
、![]() 的斜率依次成等差數(shù)列,求直線l的斜率k的取值范圍.
的斜率依次成等差數(shù)列,求直線l的斜率k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在長方體ABCD-A1B1C1D1中,底面ABCD為正方形,AA1=2,AB=1,E為AD中點,F為CC1中點.
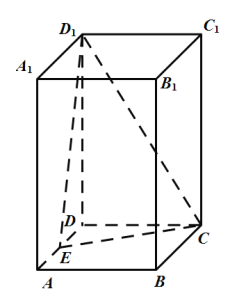
(1)求證:AD⊥D1F;
(2)求證:CE//平面AD1F;
(3)求AA1與平面AD1F成角的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com