【題目】已知定義在R上的奇函數f（x），當x≥0時，f（x）=x2﹣3x．則關于x的方程f（x）=x+3的解集為 ．
【答案】{2+ 
，﹣1，﹣3}
【解析】解：若x＜0，則﹣x＞0，
∵定義在R上的奇函數f（x），當x≥0時，f（x）=x2﹣3x．
∴當x＜0時，f（﹣x）=x2+3x=﹣f（x）．
則當x＜0時，f（x）=﹣x2﹣3x．
若x≥0，由f（x）=x+3得x2﹣3x=x+3，
則x2﹣4x﹣3=0，則x= 
= 
=2± ，
∵x≥0，∴x=2+ ，
若x＜0，由f（x）=x+3得﹣x2﹣3x=x+3，
則x2+4x+3=0，則x=﹣1或x=﹣3，
綜上方程f（x）=x+3的解集為{2+ ，﹣1，﹣3}；
所以答案是：{2+ ，﹣1，﹣3}
【考點精析】認真審題，首先需要了解函數奇偶性的性質(在公共定義域內，偶函數的加減乘除仍為偶函數；奇函數的加減仍為奇函數；奇數個奇函數的乘除認為奇函數；偶數個奇函數的乘除為偶函數；一奇一偶的乘積是奇函數;復合函數的奇偶性：一個為偶就為偶，兩個為奇才為奇)．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax3+cx（a≠0，a∈R，c∈R），當x=1時，f（x）取得極值﹣2．
（1）求函數f（x）的解析式；
（2）求函數f（x）的單調區間和極大值；
（3）若對任意x1、x2∈[﹣1，1]，不等式|f（x1）﹣f（x2）|≤t恒成立，求實數t的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對一批產品的長度（單位：毫米）進行抽樣檢測，樣本容量為400，右圖為檢測結果的頻率分布直方圖，根據產品標準，單件產品長度在區間[25，30）的為一等品，在區間[20，25）和[30，35）的為二等品，其余均為三等品，則樣本中三等品的件數為 ．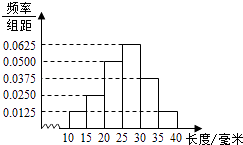 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2017湖南婁底二模】某種產品的質量以其質量指標值衡量，并依據質量指標值劃分等級如下表：
質量指標值 |
|
|
|
等級 | 三等品 | 二等品 | 一等品 |
從某企業生產的這種產品中抽取200件，檢測后得到如下的頻率分布直方圖：
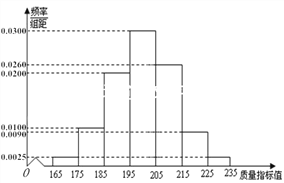
（Ⅰ）根據以上抽樣調查數據，能否認為該企業生產的這種產品符合“一、二等品至少要占全部產品92%”的規定？
（Ⅱ）在樣本中，按產品等級用分層抽樣的方法抽取8件，再從這8件產品中隨機抽取4件，求抽取的4件產品中，一、二、三等品都有的概率；
（Ⅲ）該企業為提高產品質量，開展了“質量提升月”活動，活動后在抽樣檢測，產品質量指標值
近似滿足
，則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，圓C的方程為ρ=2acosθ（a≠0），以極點為坐標原點，極軸為x軸正半軸建立平面直角坐標系，設直線l的參數方程為 
（t為參數）．
（1）求圓C的標準方程和直線l的普通方程；
（2）若直線l與圓C恒有公共點，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C的對邊分別為a，b，c，已知bcos2 
+acos2 
= 
c．
（Ⅰ）求證：a，c，b成等差數列；
（Ⅱ）若C= 
，△ABC的面積為2 
，求c．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C的兩個焦點坐標分別是F1（﹣ 
，0）、F2（ ，0），并且經過點P（ ，﹣ 
）．
（1）求橢圓C的方程；
（2）若直線l與圓O：x2+y2=1相切，并與橢圓C交于不同的兩點A、B．當 
=λ，且滿足 ≤λ≤ 
時，求△AOB面積S的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
