
【題目】已知橢圓C的兩個焦點坐標分別是F1(﹣ ![]() ,0)、F2(
,0)、F2( ![]() ,0),并且經(jīng)過點P(
,0),并且經(jīng)過點P( ![]() ,﹣
,﹣ ![]() ).
).
(1)求橢圓C的方程;
(2)若直線l與圓O:x2+y2=1相切,并與橢圓C交于不同的兩點A、B.當 ![]() =λ,且滿足
=λ,且滿足 ![]() ≤λ≤
≤λ≤ ![]() 時,求△AOB面積S的取值范圍.
時,求△AOB面積S的取值范圍.
【答案】
(1)解:設橢圓方程為: ![]() =1(a>b>0),
=1(a>b>0),
由題意可得:c= ![]() ,
, ![]() +
+ ![]() =1,a2=b2+c2,
=1,a2=b2+c2,
聯(lián)立解得:a=2,b=1.
∴橢圓C的方程為: ![]() +y2=1
+y2=1
(2)解:由題意可知:直線l的斜率不為零,
設直線l方程:x﹣my﹣n=0與圓O:x2+y2=1相切,
∴ ![]() =1,解得n2=m2+1.
=1,解得n2=m2+1.
設A(x1,y1),B(x2,y2),
聯(lián)立 ![]() ,
,
消去x整理得:(m2+4)y2+2mny+n2﹣4=0,
∴y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() .
.
又∵|AB|= ![]() |y1﹣y2|,
|y1﹣y2|,
∴ ![]() =
= ![]() ,
,
λ= ![]() =x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2=
=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2= ![]() =
= ![]() ,
,
∵ ![]() ≤λ≤
≤λ≤ ![]() ,令t=m2+1,
,令t=m2+1,
則λ= ![]() ,可得t∈[3,6],
,可得t∈[3,6],
∴S△AOB=2 ![]()
![]() =
= ![]() ,
,
∵ ![]() ∈
∈ ![]() ,∴(
,∴( ![]() +6)∈
+6)∈ ![]() ,
,
∴ ![]() ∈
∈ ![]() ,
,
∴S△AOB∈ ![]()
【解析】(1)設橢圓方程為: ![]() =1(a>b>0),由題意可得:c=
=1(a>b>0),由題意可得:c= ![]() ,
, ![]() +
+ ![]() =1,a2=b2+c2 , 聯(lián)立解出即可得出.(2)由題意可知:直線l的斜率不為零,設直線l方程:x﹣my﹣n=0與圓O:x2+y2=1相切,可得
=1,a2=b2+c2 , 聯(lián)立解出即可得出.(2)由題意可知:直線l的斜率不為零,設直線l方程:x﹣my﹣n=0與圓O:x2+y2=1相切,可得 ![]() =1.設A(x1 , y1),B(x2 , y2),直線方程與橢圓方程聯(lián)立可得:(m2+4)y2+2mny+n2﹣4=0,可得:|AB|=
=1.設A(x1 , y1),B(x2 , y2),直線方程與橢圓方程聯(lián)立可得:(m2+4)y2+2mny+n2﹣4=0,可得:|AB|= ![]() |y1﹣y2|,S△AOB=
|y1﹣y2|,S△AOB= ![]() d|AB|,λ=
d|AB|,λ= ![]() =x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2 , 由
=x1x2+y1y2=(my1+n)(my2+n)+y1y2=(m2+1)y1y2+mn(y1+y2)+n2 , 由 ![]() ≤λ≤
≤λ≤ ![]() ,令t=m2+1,則λ=
,令t=m2+1,則λ= ![]() ,可得t∈[3,6],利用基本不等式的性質(zhì)即可得出.
,可得t∈[3,6],利用基本不等式的性質(zhì)即可得出.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知定義在R上的奇函數(shù)f(x),當x≥0時,f(x)=x2﹣3x.則關(guān)于x的方程f(x)=x+3的解集為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點A(2,4),直線l:x﹣2y+1=0.
(1)求過點A且平行于l的直線的方程;
(2)若點M在直線l上,且AM⊥l,求點M的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本題滿分16分)
設函數(shù)![]() .
.
(1)若![]() =1時,函數(shù)
=1時,函數(shù)![]() 取最小值,求實數(shù)
取最小值,求實數(shù)![]() 的值;
的值;
(2)若函數(shù)![]() 在定義域上是單調(diào)函數(shù),求實數(shù)
在定義域上是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,證明對任意正整數(shù)
,證明對任意正整數(shù)![]() ,不等式
,不等式![]() 都成立.
都成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若 ![]() ,
, ![]() ,
, ![]() 為同一平面內(nèi)互不共線的三個單位向量,并滿足
為同一平面內(nèi)互不共線的三個單位向量,并滿足 ![]() +
+ ![]() +
+ ![]() =
= ![]() ,且向量
,且向量 ![]() =x
=x ![]() +
+ ![]()
![]() +(x+
+(x+ ![]() )
) ![]() (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求 ![]() 與
與 ![]() 所成角的大小;
所成角的大小;
(2)記f(x)=| ![]() |,試求f(x)的單調(diào)區(qū)間及最小值.
|,試求f(x)的單調(diào)區(qū)間及最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)g(x)滿足g(x)=g′(1)ex﹣1﹣g(0)x+ ![]() ,且存在實數(shù)x0使得不等式2m﹣1≥g(x0)成立,則m的取值范圍為( )
,且存在實數(shù)x0使得不等式2m﹣1≥g(x0)成立,則m的取值范圍為( )
A.(﹣∞,2]
B.(﹣∞,3]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】袋中有外形、質(zhì)量完全相同的紅球、黑球、黃球、綠球共12個.從中任取一球,得到紅球的概率是 ![]() ,得到黑球或黃球的概率是
,得到黑球或黃球的概率是 ![]() ,得到黃球或綠球的概率也是
,得到黃球或綠球的概率也是 ![]() .
.
(1)試分別求得到黑球、黃球、綠球的概率;
(2)從中任取一球,求得到的不是“紅球或綠球”的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校高二(1)班的一次數(shù)學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,但可見部分如圖,且將全班25人的成績記為AI(I=1,2,…,25)由右邊的程序運行后,輸出n=10.據(jù)此解答如下問題: 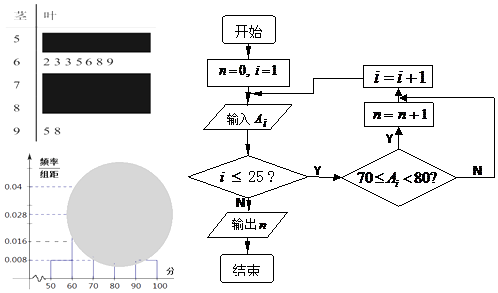
(Ⅰ)求莖葉圖中破損處分數(shù)在[50,60),[70,80),[80,90)各區(qū)間段的頻數(shù);
(Ⅱ)利用頻率分布直方圖估計該班的數(shù)學測試成績的眾數(shù),中位數(shù)分別是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分16分)已知![]() 為實數(shù),函數(shù)
為實數(shù),函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當![]() 時,令
時,令![]() ,求函數(shù)
,求函數(shù)![]() 的極值;
的極值;
(2)當![]() 時,令
時,令![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() ,使得對于函數(shù)
,使得對于函數(shù)![]() 定義域中的任意實數(shù)
定義域中的任意實數(shù)![]() ,均存在實數(shù)
,均存在實數(shù)![]() ,有
,有![]() 成立,若存在,求出實數(shù)
成立,若存在,求出實數(shù)![]() 的取值集合;若不存在,請說明理由.
的取值集合;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com